题目内容
16.(1)计算:$\sqrt{2}$sin45°+3tan30°-$\sqrt{12}$;(2)解方程:x2-6x+4=0.
分析 (1)把sin45°、tan30°的值代入代数式,化简$\sqrt{12}$后计算出最后的结果.
(2)利用配方法求出方程的解.
解答 解:(1)原式=$\sqrt{2}×\frac{\sqrt{2}}{2}$+3×$\frac{\sqrt{3}}{3}$-2$\sqrt{3}$
=1+$\sqrt{3}$-2$\sqrt{3}$
=1-$\sqrt{3}$;
(2)x2-6x=-4
x2-6x+9=5
(x-3)2=5
x-3=$±\sqrt{5}$
x=3±$\sqrt{5}$
所以x1=3+$\sqrt{5}$,x2=3-$\sqrt{5}$
点评 本题考查了特殊角的三角函数值、二次根式的运算及一元二次方程的解法.配方法的一般步骤:把常数项移到等号的右边,等号的两边都加上一次项系数一半的平方,求出x的值.

练习册系列答案
相关题目
4.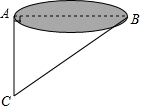 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.| A. | 75•sin55° | B. | 75•cos55° | C. | 75•tan55° | D. | $\frac{75}{tan55°}$ |
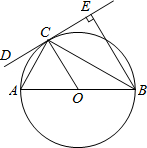 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC. (尺规作图)已知线段a,b(a<b),求作线段AB,使AB=a+b(只需画图,不要求写画法)
(尺规作图)已知线段a,b(a<b),求作线段AB,使AB=a+b(只需画图,不要求写画法)