题目内容
14.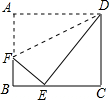 如图,将矩形纸片ABCD (AD>DC)的一角沿着过点D的直线折迭,使点A落在BC边上,落点为E,折痕交AB边交于点F.若BE:EC=1:2,则AF:FB=3:2.
如图,将矩形纸片ABCD (AD>DC)的一角沿着过点D的直线折迭,使点A落在BC边上,落点为E,折痕交AB边交于点F.若BE:EC=1:2,则AF:FB=3:2.
分析 设BE=a,EC=2a,表示出BC,根据矩形的对边相等可得AD=BC,根据翻转变换的性质可得DE=AD,AF=EF,∠DEF=∠A=90°,再求出△BEF和△CDE相似,根据相似三角形对应边成比例求解即可.
解答 解:∵BE:EC=1:2,
∴设BE=a,EC=2a,
∴BC=BE+EC=a+2a=3a,
∵四边形ABCD是矩形,
∴AD=BC=3a,
∵矩形纸片ABCD 沿着过点D的直线折叠,点A落在BC边上,落点为E,
∴DE=AD=3a,AF=EF,∠DEF=∠A=90°,
∵∠BEF+∠CED=180°-∠DEF=90°,
∠CED+∠CDE=180°-∠C=90°,
∴∠BEF=∠CDE,
又∵∠B=∠C=90°,
∴△BEF∽△CDE,
∴$\frac{EF}{DE}$=$\frac{BF}{EC}$,
∴EF:BF=DE:EC=3a:2a=3:2,
∴AF:FB=3:2.
故答案为:3:2.
点评 本题考查了矩形的性质,翻转变换的性质,相似三角形的判定与性质,翻折前后对应边相等,对应角相等,本题求出相似三角形是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
5.满足下列条件的三角形是等边三角形的个数是( )
①有两个角是60°的三角形
②有两个外角相等的等腰三角形
③腰上的高也是中线的等腰三角形
④三个外角都相等的三角形
⑤有一个角为60°的等腰三角形.
①有两个角是60°的三角形
②有两个外角相等的等腰三角形
③腰上的高也是中线的等腰三角形
④三个外角都相等的三角形
⑤有一个角为60°的等腰三角形.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6. a,b在数轴上的位置如图,化简|a-b|-|b+a|=( )
a,b在数轴上的位置如图,化简|a-b|-|b+a|=( )
 a,b在数轴上的位置如图,化简|a-b|-|b+a|=( )
a,b在数轴上的位置如图,化简|a-b|-|b+a|=( )| A. | 2b-a | B. | -a | C. | -2b-2a | D. | -2a |
3.已知|a|=5,|b|=3,且a+b<0,则a-b的值为( )
| A. | -8 | B. | +2 | C. | -8或-2 | D. | -2或+8 |