题目内容
4.计算:$\frac{1}{{1+\sqrt{3}}}$+$\frac{1}{{\sqrt{3}+\sqrt{5}}}$+$\frac{1}{{\sqrt{5}+\sqrt{7}}}$+…+$\frac{1}{{\sqrt{79}+\sqrt{81}}}$=4.分析 首先把每个式子分母有理化,化成根式的和、差形式即可化简求解.
解答 解:原式=$\frac{\sqrt{3}-1}{2}$+$\frac{\sqrt{5}-\sqrt{3}}{2}$+$\frac{\sqrt{7}-\sqrt{5}}{2}$+…+$\frac{\sqrt{81}-\sqrt{79}}{2}$
=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{5}}{2}$-$\frac{\sqrt{5}}{2}$+$\frac{\sqrt{7}}{2}$-…-$\frac{\sqrt{79}}{2}$+$\frac{\sqrt{81}}{2}$
=-$\frac{1}{2}$+$\frac{\sqrt{81}}{2}$
=-$\frac{1}{2}$+$\frac{9}{2}$
=4.
故答案是:4.
点评 本题考查了二次根式的混合运算,正确对二次根式进行分母有理化是关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
12.下列函数中,当x>0时,y随x的增大而减小的是( )
| A. | y=2x2 | B. | y=2x-1 | C. | y=$\frac{-2}{x}$ | D. | y=-2x2 |
19.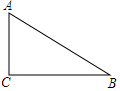 如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
 如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心,4为半径作⊙A,则( )| A. | 点B在⊙A外 | B. | 点B在⊙A上 | ||
| C. | 点B在⊙A外内 | D. | 点B与⊙A的位置关系不能确定 |
13. 如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A与原起点B的距离AB(精确到0.1米).
 如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°. | 参考数据 | α=5° | α=12° | |
| sinα | 0.09 | 0.21 | |
| cosα | 0.10 | 0.98 | |
| tanα | 0.09 | 0.21 |
(2)求斜坡新起点A与原起点B的距离AB(精确到0.1米).
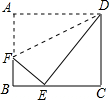 如图,将矩形纸片ABCD (AD>DC)的一角沿着过点D的直线折迭,使点A落在BC边上,落点为E,折痕交AB边交于点F.若BE:EC=1:2,则AF:FB=3:2.
如图,将矩形纸片ABCD (AD>DC)的一角沿着过点D的直线折迭,使点A落在BC边上,落点为E,折痕交AB边交于点F.若BE:EC=1:2,则AF:FB=3:2.