题目内容
16.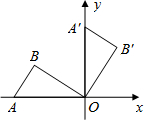 如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.
如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.(1)求B′点的坐标.
(2)以原点为对称中心,请写出与△A′OB′成中心对称的三角形的顶点坐标.
分析 (1)根据直角三角形30°角所对的直角边等于斜边的一半可得OA=2AB,再求出OB,根据旋转的性质可得OB′=OB,过点B′作B′C⊥x轴于C,求出∠COB′=60°,然后求出OC、B′C,再根据点的坐标的定义求解即可;
(2)根据旋转的性质可得OA′=OA,然后写出点A′的坐标,再根据关于原点对称的点的横坐标与纵坐标都互为相反数求解.
解答 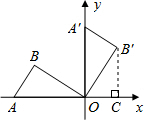 解:(1)∵∠AOB=30°,∠B=90°,
解:(1)∵∠AOB=30°,∠B=90°,
∴OA=2AB=2×1=2,
OB=$\sqrt{3}$AB=$\sqrt{3}$,
∵△AOB绕O点顺时针旋转90°得△A′OB′,
∴OB′=OB=$\sqrt{3}$,
过点B′作B′C⊥x轴于C,
则∠COB′=180°-30°-90°=60°,
∴OC=$\frac{1}{2}$OB′=$\frac{\sqrt{3}}{2}$,
B′C=$\frac{\sqrt{3}}{2}$OB′=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$=$\frac{3}{2}$,
所以,点B′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$);
(2)∵△AOB绕O点顺时针旋转90°得△A′OB′,
∴OA′=OA=2,
∴点A′的坐标为(0,2),
∴△A′OB′关于原点成中心对称的三角形的顶点坐标分别为(0,-2),(0,0),(-$\frac{\sqrt{3}}{2}$,-$\frac{3}{2}$).
点评 本题考查了坐标与图形的变化-旋转,直角三角形30°角所对的直角边等于斜边的一半的性质,关于原点对称的点的坐标特征,解题的关键在于作出以点B′为顶点的直角三角形.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
1.一颗木质的中国象棋子“车”,它的正面雕刻一个“车”字,它的反面是平的,将它从一定高度掷下,落地反弹后可能是“车”字面朝上,也可能是“车”字面朝下,由于棋子的两面不均匀,为了估计“车”字面朝上的概率,七年级某实验小组做了掷棋子的试验,试验数据如下表:
(1)请将数据表补充完整;
(2)根据上表,画出“车”字面朝上的频率的折线统计图;
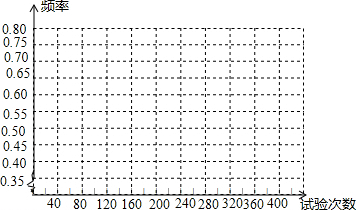
(3)如将试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少?
| 试验次数 | 20 | 80 | 100 | 160 | 200 | 240 | 300 | 360 | 400 |
| “车”字朝上的频数 | 14 | 48 | 50 | 84 | 112 | 144 | 172 | 204 | 228 |
| 相应的频率 | 0.70 | 0.60 | 0.50 | 0.53 | 0.56 | 0.60 | 0.57 | 0.57 | 0.57 |
(2)根据上表,画出“车”字面朝上的频率的折线统计图;

(3)如将试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少?
6.计算90°-18°50′45″的结果正确的是( )
| A. | 71°9′15″ | B. | 72°9′15″ | C. | 72°10′15″ | D. | 71°10′15″ |