题目内容
7.解方程组$\left\{\begin{array}{l}{|x+5|+y=4x-1}\\{|2x-4|+|y-4|=3x}\end{array}\right.$.分析 根据绝对值的性质,可化简方程组,根据解方程组,可得答案.
解答 解:当x<-5,y<4时,$\left\{\begin{array}{l}{-x-5+y=4x-1}\\{-2x+4-y+4=3x}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{7}{5}}\\{y=11}\end{array}\right.$不符合题意舍;
当x<-5,y≥4时,$\left\{\begin{array}{l}{-x-5+y=4x-1}\\{-2x+4+y-4=3x}\end{array}\right.$方程组无解,
当-5≤x<2,y<4时,$\left\{\begin{array}{l}{x+5+y=4x-1}\\{-2x+4-y+4=3x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{7}{4}}\\{y=-\frac{3}{4}}\end{array}\right.$;
当-5≤x<2,y≥4时,$\left\{\begin{array}{l}{x+5+y=4x-1}\\{-2x+4+y-4=3x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=-\frac{23}{2}}\end{array}\right.$不符合题意舍;
当x≥2,y<4时,$\left\{\begin{array}{l}{x+5+y=4x-1}\\{2x-4-y+4=3x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{3}{2}}\end{array}\right.$不符合题意舍;
当x≥2,y≥4时,$\left\{\begin{array}{l}{x+5+y=4x-1}\\{2x-4+y-4=3x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=7}\\{y=15}\end{array}\right.$,
原方程组的解为$\left\{\begin{array}{l}{x=\frac{7}{4}}\\{y=-\frac{3}{4}}\end{array}\right.$,$\left\{\begin{array}{l}{x=7}\\{y=15}\end{array}\right.$.
点评 本题考查了解二元一次方程组,分类讨论是解题关键,以防遗漏.

| A. | (1,2) | B. | (-1,-8) | C. | (0,-3) | D. | (2,-7) |
| A. | a5+a5=a10 | B. | a6-a4=a24 | C. | a6•a4=a24 | D. | a8÷a5=a3 |
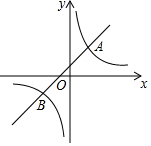 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.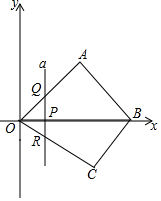 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.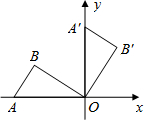 如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.
如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.