题目内容
6.先化简,再求值:(1)(1+$\frac{1}{x-1}$)÷$\frac{x}{{{x^2}-1}}$,其中x=-2;
(2)($\frac{{{a^2}+2a+1}}{{{a^2}-1}}$-$\frac{1}{a-1}$)÷$\frac{a^2}{a-1}$,选一个你喜欢的a值代入求值.
分析 根据分式的运算法则即可求出答案.
解答 解:(1)当x=-2时,
原式=$\frac{x}{x-1}$×$\frac{(x+1)(x-1)}{x}$=x+1=-1
(2)当a=2时,
原式=[$\frac{(a+1)^{2}}{(a-1)(a+1)}$-$\frac{1}{a-1}$]×$\frac{a-1}{{a}^{2}}$
=($\frac{a+1}{a-1}$-$\frac{1}{a-1}$)×$\frac{a-1}{{a}^{2}}$
=$\frac{1}{a}=\frac{1}{2}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知m是方程x2+x-5=0的一个根,则代数式m2+m的值等于( )
| A. | -5 | B. | 5 | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
7.下列各点不在直线y=5x-3上的是( )
| A. | (1,2) | B. | (-1,-8) | C. | (0,-3) | D. | (2,-7) |
11.下列说法正确的是( )
| A. | a、b、c是直线,若a⊥b,b∥c,则a∥c | B. | a、b、c是直线,若a⊥b,b⊥c,则a⊥c | ||
| C. | a、b、c是直线,若a∥b,b⊥c,则a∥c | D. | a、b、c是直线,若a∥b,b∥c,则a∥c |
 已知:点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连接AD,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.
已知:点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连接AD,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.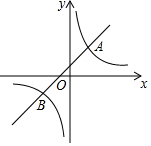 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.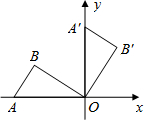 如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.
如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.