题目内容
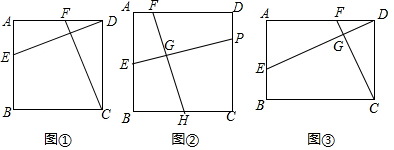
8.(一)问题初探:(1)如图①,在正方形ABCD中,点E,F分别在AB,AD上,且DE⊥CF.则DE与CF的数量关系是DE=CF;
(二)类比探究:
(2)如图②,在正方形ABCD中,点E,H,P,F分别在AB,BC,CD,DA上,若HF⊥EP于点G,探究线段HF与EP的数量关系,并说明理由;
(三)拓展延伸:
(3)如图③,在矩形ABCD中,AB=m,AD=n,且DE⊥CF,则$\frac{DE}{CF}$=$\frac{n}{m}$.(用含m,n的代数式表示)
分析 (一)问题初探:根据正方形的性质,DE上CF,证明△AED≌DFC,即可解答;
(二)类比延伸如图②中,作FM⊥BC于M,PN⊥AB于N,则四边形ABMF,ANPD都是矩形.只要证明△HMF≌△ENP即可解决问题;
(三)拓展探究:根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;
解答 解:(一)问题初探:结论:DE=CF.
理由:如图①中,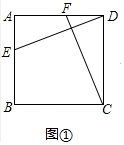
∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,AD=CD,
∵CF⊥DE,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
在△AED和DFC中,
$\left\{\begin{array}{l}{∠A=∠FDC}\\{∠CFD=∠AED}\\{AD=CD}\end{array}\right.$,
∴△AED≌DFC,
∴DE=CF.
故答案为:DE=CF.
(二)类比探究:结论:PE=EH.
理由:如图②中,作FM⊥BC于M,PN⊥AB于N,则四边形ABMF,ANPD都是矩形.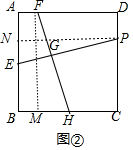
∴FM=PN,∠HMF=∠ENP,
∵HF⊥EP,∠B=90°,
∴∠GHM+∠GEB=180°,
又∵∠NEP+∠GEB=180°,
∴∠GHM=∠NEP,
∴△HMF≌△ENP(AAS),
∴HF=EP.
(三)拓展延伸:如图③中,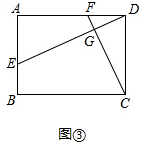
∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,AB=CD=m,
∵CF⊥DE,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
∵∠A=∠CDF,
∴△AED∽△DFC,
∴$\frac{DE}{CF}$=$\frac{AD}{CD}$=$\frac{n}{m}$,
故答案为:$\frac{n}{m}$.
点评 本题考查了矩形性质和判定,勾股定理,正方形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定的应用,主要考查学生综合运用性质和定理进行推理的能力,题目比较好.

| A. | 全等的三角形 | B. | 全等的四边形 | C. | 全等的正五边形 | D. | 全等的正六边形 |
| 组别 | A型 | B型 | AB型 | O型 |
| 频数 | b | c | d | 6 |
| 频率 | a | 0.35 | 0.1 | e |
| A. | 16人 | B. | 14人 | C. | 4人 | D. | 6人 |
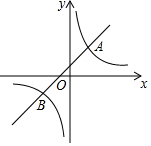 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.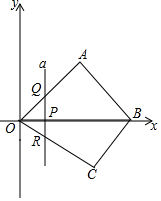 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.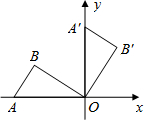 如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.
如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.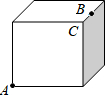 在正方体的一个顶点A处有一只蚂蚁,现在要向点B处爬行,已知正方体的棱长为3cm,BC=1cm,则爬行的最短距离是多少?
在正方体的一个顶点A处有一只蚂蚁,现在要向点B处爬行,已知正方体的棱长为3cm,BC=1cm,则爬行的最短距离是多少?