题目内容
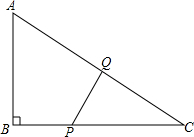 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:(1)经过多少秒后,PQ平分△ABC的面积;
(2)经过多少秒后,△CPQ为直角三角形.
考点:一元二次方程的应用
专题:几何动点问题
分析:(1)可设经过x秒后,PQ平分△ABC的面积,根据速度×时间=路程和三角函数分别表示出△CPQ中PC边和PC边高的长度,再分两种情况:Q在AC边;Q在AB边;根据三角形面积公式即可求解;
(2)可设经过y秒后,△CPQ为直角三角形,根据速度×时间=路程分别表示出△CPQ中PC边和QC边,再根据三角函数分两种情况:∠PQC=90°;∠QPC=90°;即可求解.
(2)可设经过y秒后,△CPQ为直角三角形,根据速度×时间=路程分别表示出△CPQ中PC边和QC边,再根据三角函数分两种情况:∠PQC=90°;∠QPC=90°;即可求解.
解答:解:∵在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,
∴AC=
=10厘米.
(1)设经过x秒后,PQ平分△ABC的面积,依题意有
Q在AC边:
(8-x)×(
×2x)=
×
×8×6,
化简得x2-8x+24=0,
∵△=82-4×24=-32<0,
∴方程无解;
Q在AB边:
(8-x)×(6+10-2x)=
×
×8×6,
解得x1=8+2
(不合题意舍去),x2=8-2
(不合题意舍去).
(2)设经过y秒后,△CPQ为直角三角形,依题意有
当∠PQC=90°时,
×(8-y)=2y,解得y=
;
当∠QPC=90°时,8-y=
×2y,解得y=4(
-1).
综上所述,经过
秒或4(
-1)秒后,△CPQ为直角三角形.
∴AC=
| 62+82 |
(1)设经过x秒后,PQ平分△ABC的面积,依题意有
Q在AC边:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
化简得x2-8x+24=0,
∵△=82-4×24=-32<0,
∴方程无解;
Q在AB边:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得x1=8+2
| 3 |
| 3 |
(2)设经过y秒后,△CPQ为直角三角形,依题意有
当∠PQC=90°时,
| ||
| 2 |
32
| ||
| 13 |
当∠QPC=90°时,8-y=
| ||
| 2 |
| 3 |
综上所述,经过
32
| ||
| 13 |
| 3 |
点评:本题考查了三角形的面积公式的运用,列一元二次方程解设计问题的运用,一元二次方程的解法的运用,解答时根据三角形的面积公式建立方程是关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
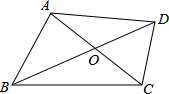 如图,四边形ABCD的对角线AC、BD交于点O,且BD平分AC.若BD=10,AC=6,∠BOC=120°,则四边形ABCD的面积为
如图,四边形ABCD的对角线AC、BD交于点O,且BD平分AC.若BD=10,AC=6,∠BOC=120°,则四边形ABCD的面积为 ”图案.
”图案.
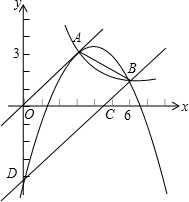 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).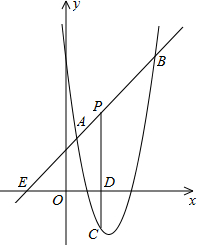 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( 如图,一次函数y=(m-1)x+3的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为
如图,一次函数y=(m-1)x+3的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为