题目内容
 如图,一次函数y=(m-1)x+3的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为
如图,一次函数y=(m-1)x+3的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为| 9 |
| 4 |
(1)求m的值及点A的坐标;
(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=2OA,求直线BP的函数表达式.
考点:两条直线相交或平行问题
专题:
分析:(1)求出点B的坐标,然后求出OB,再利用三角形的面积求出OA,从而得到点A的坐标,再代入直线解析式求解即可得到m的值;
(2)求出点P的坐标,再利用待定系数法求一次函数解析式解答.
(2)求出点P的坐标,再利用待定系数法求一次函数解析式解答.
解答:解:(1)由点B(0,3)得OB=3,
∵S△OAB=
,
∴
×OA×OB=
,
解得OA=
,
∴A(-
,0),
把点A(-
,0)代入y=(m-1)x+3,得m=3;
(2)∵OP=2OA,
∴OP=3,
∴点P的坐标为(3,0),
设直线BP的函数表达式为y=kx+b,代入P(3,0)、B(0,3),
得
,
解得
,
所以,直线BP的函数表达式为y=-x+3.
∵S△OAB=
| 9 |
| 4 |
∴
| 1 |
| 2 |
| 9 |
| 4 |
解得OA=
| 3 |
| 2 |
∴A(-
| 3 |
| 2 |
把点A(-
| 3 |
| 2 |
(2)∵OP=2OA,
∴OP=3,
∴点P的坐标为(3,0),
设直线BP的函数表达式为y=kx+b,代入P(3,0)、B(0,3),
得
|
解得
|
所以,直线BP的函数表达式为y=-x+3.
点评:本题考查了两直线相交的问题,主要利用了待定系数法求一次函数解析式,三角形的面积,得到点B的坐标是解题的关键.

练习册系列答案
相关题目
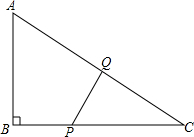 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问: 如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为
如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为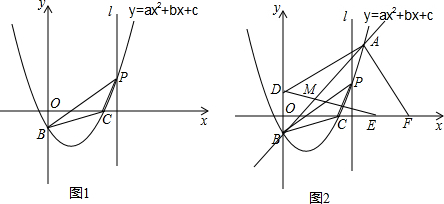
 用圆规、直尺作图,不写作法,但要保留作图痕迹.在一块三角形废料上,要裁下一个圆形的材料,并且要尽可能的充分利用好原三角形废料,请画出这个圆形.
用圆规、直尺作图,不写作法,但要保留作图痕迹.在一块三角形废料上,要裁下一个圆形的材料,并且要尽可能的充分利用好原三角形废料,请画出这个圆形.