题目内容
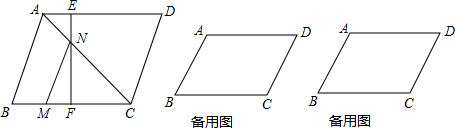
如图所示：已知四边形ABCD为菱形，AB=10，tanB=
，E是AD边上一个动点（点E与点A不重合），过E作EF⊥BC，交边BC于点F．
（1）求EF的长；
（2）连接AC交EF于点N，M是BC边上一动点，且CM=2AE，设AE=x，△CMN的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；
（3）当AE为何值时，△CMN是以MN为腰的等腰三角形？
| 4 |
| 3 |
（1）求EF的长；
（2）连接AC交EF于点N，M是BC边上一动点，且CM=2AE，设AE=x，△CMN的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；
（3）当AE为何值时，△CMN是以MN为腰的等腰三角形？
考点：相似三角形的判定与性质,菱形的性质,解直角三角形
专题：
分析：（1）作AG⊥BC于G，根据AB=10，tanB=
，通过解直角三角形求得AG，然后根据平行线间的距离相等得出EF=AG即可；
（2）根据平行线分线段成比例定理即可求得
=2，然后通过三角形相似对应边成比例求得
=
=2，进而求得FN=8-2x，从而求得三角形的面积；
（3）通过三角形全等求得EN=FN=4，根据（2）求得的EN=2AE即可求得；
| 4 |
| 3 |
（2）根据平行线分线段成比例定理即可求得
| FN |
| CF |
| EN |
| AE |
| FN |
| FC |
（3）通过三角形全等求得EN=FN=4，根据（2）求得的EN=2AE即可求得；
解答：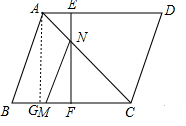
解：（1）作AG⊥BC于G，
∵tanB=
，
∴
=
，
∴AB=10，
∴AG=8，BG=6，
∴CG=10-6=4，
∵AG⊥BC，EF⊥BC，
∴EF∥AG，EF=AG=8，
（2）∵EF∥AG，
∴
=
，
即
=
，
∴
=2，
∵四边形ABCD为菱形，
∴AD∥BC，
∴△AEN∽△CFN，
∴
=
，
∴
=
=2，
∴EN=2AE=2x，
∴FN=EF-EN═8-2x，
∴y=
×2x（8-2x）=-2x2+8x，
即y=-2x2+8x（0＜x＜5）；
（3）∵△CMN是以MN为腰的等腰三角形，EF⊥BC，
∴MF=CF，
∵CM=2AE，
∴MF=CF=AE，
在△AEN与△CFN中，
，
∴△AEN≌△CFN（AAS），
∴EN=FN=
EF=4，
由（2）可知：EN=2AE，
∴AE=
EN=2；
解：（1）作AG⊥BC于G，∵tanB=
| 4 |
| 3 |
∴
| AG |
| BG |
| 4 |
| 3 |
∴AB=10，
∴AG=8，BG=6，
∴CG=10-6=4，
∵AG⊥BC，EF⊥BC，
∴EF∥AG，EF=AG=8，
（2）∵EF∥AG，
∴
| CF |
| CG |
| FN |
| AM |
即
| CF |
| 4 |
| FN |
| 8 |
∴
| FN |
| CF |
∵四边形ABCD为菱形，
∴AD∥BC，
∴△AEN∽△CFN，
∴
| FC |
| AE |
| FN |
| EN |
∴
| EN |
| AE |
| FN |
| FC |
∴EN=2AE=2x，
∴FN=EF-EN═8-2x，
∴y=
| 1 |
| 2 |
即y=-2x2+8x（0＜x＜5）；
（3）∵△CMN是以MN为腰的等腰三角形，EF⊥BC，
∴MF=CF，
∵CM=2AE，
∴MF=CF=AE，
在△AEN与△CFN中，
|
∴△AEN≌△CFN（AAS），
∴EN=FN=
| 1 |
| 2 |
由（2）可知：EN=2AE，
∴AE=
| 1 |
| 2 |
点评：本题考查了菱形的性质，解直角三角形，等腰直角三角形的判定和性质，相似三角形的判定和性质，平行线分线段定理等；本题的关键是找出EN=2AE的关系．
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
若式子
有意义，则m、n应满足（ ）
|
| A、m≥0且n≥0 |
| B、m、n同号 |
| C、m≥0且n＞0 |
| D、m•n≥0且m≠0 |
如图，在?ABCD中，F是AD的中点，延长BC到点E，使CE=