题目内容
1.问题背景:在△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上:$\frac{7}{2}$.
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别为$\sqrt{5}$a、$\sqrt{8}$a、$\sqrt{17}$a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为$\sqrt{{m}^{2}+16{n}^{2}}$、$\sqrt{9{m}^{2}+4{n}^{2}}$、$\sqrt{16{m}^{2}+4{n}^{2}}$ (m>0,n>0,且m≠n),试运用构图法画出示意图并求出这三角形的面积.
分析 (1)△ABC的面积=3×3-1×2÷2-1×3÷2-2×3÷2=$\frac{7}{2}$;
(2)$\sqrt{5}$a是直角边长为a,2a的直角三角形的斜边;$\sqrt{8}$a是直角边长为2a,2a的直角三角形的斜边;$\sqrt{17}$a是直角边长为a,4a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为m,4n的直角三角形的斜边;直角边长为3m,2n的直角三角形的斜边;直角边长为4m,2n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
解答 解:(1)S△ABC=3×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×3=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
(2)如图1,在边长为a的正方形网格中,△ABC即为所求作三角形,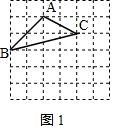
S△ABC=2a×4a-$\frac{1}{2}$×2a×2a-$\frac{1}{2}$×2a×a-$\frac{1}{2}$×4a×a=3a2;
(3)如图2,在长为m、宽为n的网格中,△ABC即为所求作三角形,
其中AB=$\sqrt{{m}^{2}+16{n}^{2}}$、AC=$\sqrt{9{m}^{2}+4{n}^{2}}$、BC=$\sqrt{16{m}^{2}+4{n}^{2}}$,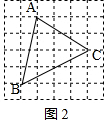
S△ABC=4m×4n-$\frac{1}{2}$×m×4n-$\frac{1}{2}$×3m×2n-$\frac{1}{2}$×4m×2n=7mn.
点评 此题主要考查了勾股定理应用,利用了数形结合的思想,通过构造直角三角形,利用勾股定理求解是解题关键.关键是结合网格用矩形及容易求得面积的直角三角形表示出所求三角形的面积进行解答.

 名校课堂系列答案
名校课堂系列答案 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.| A. | 16-8$\sqrt{3}$ | B. | -12+8$\sqrt{3}$ | C. | 8-4$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
 在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$.
在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$.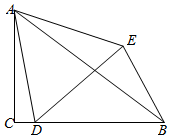 在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.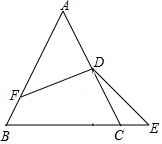 已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.
已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$. 将一副三角尺按如图方式进行摆放,则∠1的度数为120°.
将一副三角尺按如图方式进行摆放,则∠1的度数为120°. 已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.
已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.