题目内容
16.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB落在AD边上,折痕为AE,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则FC:CD的值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.
解答 解:由题意知:AB=BE=6,BD=AD-AB=2,AD=AB-BD=4;
∵CE∥AB,
∴△ECF∽△ADF,
∴$\frac{CE}{AD}$=$\frac{1}{2}$,即DF=2CF,
∴CF:CD=1:3;
故选:B.
点评 本题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,数掌握相似三角形的判断和性质是解题的关键.

练习册系列答案
相关题目
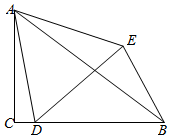 在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.
 如图,已知圆O,弦AB、CD相交于点M.
如图,已知圆O,弦AB、CD相交于点M.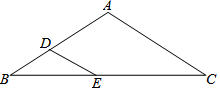 已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.
已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点. 海关缉私人员驾艇在C处发现正北方向30km的A处有一艘可疑船只,并测得它正以60km/h的速度向北偏东60°的方向航行,缉私艇随即以90km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?(结果保留根号)
海关缉私人员驾艇在C处发现正北方向30km的A处有一艘可疑船只,并测得它正以60km/h的速度向北偏东60°的方向航行,缉私艇随即以90km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?(结果保留根号) 如图,已知四边形ABCD和点O,画四边形EFGH,使四边形EFGH和四边形ABCD关于点O成中心对称.
如图,已知四边形ABCD和点O,画四边形EFGH,使四边形EFGH和四边形ABCD关于点O成中心对称.