题目内容
7.(1)解分式方程:$\frac{x}{x-1}-\frac{2}{x}$=1;(2)解不等式组:$\left\{\begin{array}{l}2x-1>0\\ x-3(x-2)≥4\end{array}$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母得:x2-2x+2=x2-x,
解得:x=2,
经检验x=2是分式方程的解;
(2)$\left\{\begin{array}{l}{2x-1>0①}\\{x-3(x-2)≥4②}\end{array}\right.$,
由①得:x>$\frac{1}{2}$,
由②得:x≤1,
则不等式组的解集为$\frac{1}{2}$<x≤1.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
17. 如图,在方格纸上有一个三角形ABC,则这个三角形是( )
如图,在方格纸上有一个三角形ABC,则这个三角形是( )
 如图,在方格纸上有一个三角形ABC,则这个三角形是( )
如图,在方格纸上有一个三角形ABC,则这个三角形是( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 不能确定 |
2.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定9名同学参加决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
12.新京报讯,2015年全国春运进入节前返程高峰,南京的旅客维持在超过50万人的数量,而全国预计发送旅客突破770万人次,将770万用科学记数法表示为( )
| A. | 77×105 | B. | 7.7×106 | C. | 7.7×105 | D. | 0.77×106 |
19.在平面直角坐标系中,先将抛物线y=x2+bx-c关于x轴作轴对称变换,再将所得的抛物线关于y轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为( )
| A. | y=x2+bx-c | B. | y=x2-bx+c | C. | y=-x2+bx+c | D. | y=-x2+bx-c |
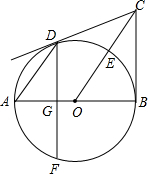 如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.
如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.