题目内容
15.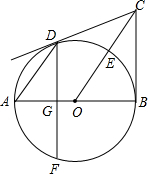 如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.
如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.(1)求证:OC垂直平分BD,
(2)求证:CD是⊙O的切线;
(3)若cos∠BAD=$\frac{3}{5}$,⊙O的半径为5,求DF的长.
分析 (1)根据AD∥OC可得∠A=∠COB,OC⊥BD,从而判定$\widehat{DE}$=$\widehat{BE}$,根据垂径定理即可证得OC垂直平分BD;
(2)连接OD,只要证明∠CDO=90°即可;
(3)在△ADG中用勾股定理求解.
解答 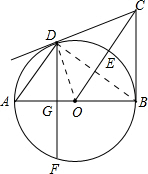 (1)证明:连接OD,BD;
(1)证明:连接OD,BD;
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AD∥OC,
∴∠A=∠COB,
∵∠A=$\frac{1}{2}$∠BOD,
∴∠BOC=$\frac{1}{2}$∠BOD;
∴∠DOC=∠BOC;
∴$\widehat{DE}$=$\widehat{BE}$,
∴OC垂直平分BD.
(2)证明:如图所示:
由(1)知∠DOE=∠BOE,
在△COD和△COB中
$\left\{\begin{array}{l}{OD=OB}\\{∠DOE=∠BOE}\\{OC=OC}\end{array}\right.$
∴△COD≌△COB(SAS);
∴∠CDO=∠B;
又∵BC⊥AB,
∴∠CDO=∠B=90°;
∴CD是⊙O的切线;
(3)解:在△ADG中,∵cos∠BAD=$\frac{AG}{AD}$,
设AG=3x,AD=5x;
∵DF⊥AB,
∴DG=4x;
又∵⊙O的半径为5,
∴OG=5-3x;
∵OD2=DG2+OG2,
∴52=(4x)2+(5-3x)2;
∴x1=$\frac{6}{5}$,x2=0;(舍去)
∴DF=2DG=2×4x=8x=8×$\frac{6}{5}$=$\frac{48}{5}$.
点评 本题综合考查了切线的判定与性质、圆周角定理以及勾股定理.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
3.计算-2+1的结果是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
10.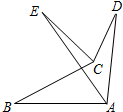 如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )
如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )
 如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )
如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )| A. | ∠AEC=∠ABC-2∠ADC | B. | ∠AEC=$\frac{∠ABC-∠ADC}{2}$ | ||
| C. | ∠AEC=$\frac{1}{2}$∠ABC-∠ADC | D. | ∠AEC=$\frac{∠ABC-∠ADC}{3}$ |
20.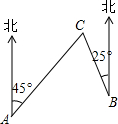 如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
 如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )| A. | 70° | B. | 20° | C. | 35° | D. | 110° |
3. 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )
如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )
 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )
如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
