题目内容
18．圆锥体的高h=2$\sqrt{3}$cm，底面圆半径r=2cm，则圆锥体的全面积为12πcm2．分析 表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2．
解答 解：底面圆的半径为2，则底面周长=4π，
∵底面半径为2cm、高为2$\sqrt{3}$cm，
∴圆锥的母线长为4cm，
∴侧面面积=×4π×4=8π；
底面积为=4π，
全面积为：8π+4π=12πcm2．
故答案为：12π．
点评 本题利用了圆的周长公式和扇形面积公式求解，牢记公式是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．计算-2+1的结果是（ ）
| A． | -1 | B． | -3 | C． | 1 | D． | 3 |
10．
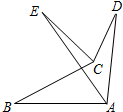如图，∠ABC＞∠ADC，且∠BAD的平分线AE与∠BCD的平分线CE交于点E，则∠AEC与∠ADC、∠ABC之间存在的等量关系是（ ）
如图，∠ABC＞∠ADC，且∠BAD的平分线AE与∠BCD的平分线CE交于点E，则∠AEC与∠ADC、∠ABC之间存在的等量关系是（ ）| A． | ∠AEC=∠ABC-2∠ADC | B． | ∠AEC=$\frac{∠ABC-∠ADC}{2}$ | ||
| C． | ∠AEC=$\frac{1}{2}$∠ABC-∠ADC | D． | ∠AEC=$\frac{∠ABC-∠ADC}{3}$ |
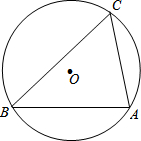对于一个三角形，设其三个内角的度数分别为x°、y°和z°，若x、y、z满足x2+y2=z2，我们定义这个三角形为美好三角形．