题目内容

19．在平面直角坐标系中，先将抛物线y=x2+bx-c关于x轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（　　）
A．y=x2+bx-cB．y=x2-bx+cC．y=-x2+bx+cD．y=-x2+bx-c

分析 根据平面直角坐标系中，二次函数关于x轴、y轴轴对称的特点得出答案．

解答 解：先将抛物线y=x2+bx-c关于x轴作轴对称变换，可得新抛物线为y=-x2-bx+c；再将所得的抛物线y=-x2-bx+c关于y轴作轴对称变换，可得新抛物线为y=-x2+bx+c．
故选：C．

点评 本题考查的是二次函数的图象与几何变换，熟知关于x轴、y对称的点的坐标特点是解答此题的关键．

练习册系列答案
相关题目
9．不等式$\frac{3x+1}{2}$-5≤3的正整数解的和为15．
10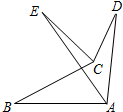．如图，∠ABC＞∠ADC，且∠BAD的平分线AE与∠BCD的平分线CE交于点E，则∠AEC与∠ADC、∠ABC之间存在的等量关系是（　　）
A．∠AEC=∠ABC-2∠ADCB．∠AEC=$\frac{∠ABC-∠ADC}{2}$
C．∠AEC=$\frac{1}{2}$∠ABC-∠ADCD．∠AEC=$\frac{∠ABC-∠ADC}{3}$
7．（1）解分式方程：$\frac{x}{x-1}-\frac{2}{x}$=1；
（2）解不等式组：$\left\{\begin{array}{l}2x-1＞0\\ x-3（x-2）≥4\end{array}$．
14．函数y=$\frac{1}{\sqrt{x}-1}$的自变量x的取值范围是x＞1．
2．如图1，抛物线y=ax2-3ax-4a（a＜0）交x轴于点A、B（A左B右），交y轴正半轴于点C．
（1）求A、B两点的坐标；
（2）点D在抛物线在第一象限的部分上一动点，当∠ACB=90°时，
①求抛物线的解析式；
②当四边形OCDB的面积最大时，求点D的坐标；
③如图2，若E为BC的中点，DE的延长线交线段AB于点F，当△BEF为钝角三角形时，请直接写出点D的纵坐标y的范围．
9．在Rt△ABC中，∠C=90°，AB=10，AC=6，以C为圆心作⊙C和AB相切，则⊙C的半径长为4.8．
6．对于一个三角形，设其三个内角的度数分别为x°、y°和z°，若x、y、z满足x2+y2=z2，我们定义这个三角形为美好三角形．
（1）△ABC中，若∠A=50°，∠B=70°，则△ABC不是（填“是”或“不是”）美好三角形；
（2）如图，锐角△ABC是⊙O的内接三角形，∠C=60°，AC=4，⊙O的直径是$4\sqrt{2}$，求证：△ABC是美好三角形；
（3）已知△ABC是美好三角形，∠A=30°，求∠C的度数．
7．下列命题的逆命题是假命题的是（　　）
A．两直线平行，同位角相等B．平行四边形的对角线互相平分
C．菱形的四条边相等D．正方形的四个角都是直角

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网