题目内容

15．若有公式（a+b）3=a3+3a2b+3ab2+b3，则我们在利用该公式探索（a-b）3的结果时，可将（a-b）3首先转化为[a+（-b）]3．

分析 根据已知公式将原式转化为和的立方即可．

解答 解：（a-b）3=[a+（-b）]3．
故答案为：[a+（-b）]3．

点评 此题考查了完全平方公式，灵活运用题中公式是解本题的关键．

练习册系列答案
相关题目
7．（1）解分式方程：$\frac{x}{x-1}-\frac{2}{x}$=1；
（2）解不等式组：$\left\{\begin{array}{l}2x-1＞0\\ x-3（x-2）≥4\end{array}$．
6．对于一个三角形，设其三个内角的度数分别为x°、y°和z°，若x、y、z满足x2+y2=z2，我们定义这个三角形为美好三角形．
（1）△ABC中，若∠A=50°，∠B=70°，则△ABC不是（填“是”或“不是”）美好三角形；
（2）如图，锐角△ABC是⊙O的内接三角形，∠C=60°，AC=4，⊙O的直径是$4\sqrt{2}$，求证：△ABC是美好三角形；
（3）已知△ABC是美好三角形，∠A=30°，求∠C的度数．
3．如图，在△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于F，则$\frac{DF}{AD}$=（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{2}{3}$
10．下列各方程中是二元一次方程的是（　　）
A．$\frac{x}{2}$+$\frac{y}{4}$=-1B．xy+z=5C．2x2+3y-5=0D．2x+$\frac{1}{y}$=2
20．先化简，再求值：（2a+1）2-2（2a+1）+3，其中a=-$\frac{1}{2}$．
7．下列命题的逆命题是假命题的是（　　）
A．两直线平行，同位角相等B．平行四边形的对角线互相平分
C．菱形的四条边相等D．正方形的四个角都是直角
4．在等式a•a2•（　　）=a11中，括号里填入的代数式应当是（　　）
A．a7B．a8C．a6D．a3
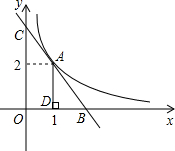5．直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$只有一个交点A（1，2），且与x轴y轴分别交于B、C两点，AD垂直平分OB，垂足为D，则直线BC的解析式为y=-2x+4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网