题目内容
14.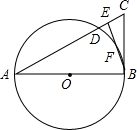 如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=$\frac{1}{2}$∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=$\frac{1}{2}$∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.(1)求证:BC与⊙O相切;
(2)连接BD,求∠ADB的度数;
(3)若AB=8,sin∠EBC=$\frac{1}{4}$,求AC的长.
分析 (1)首先连接AF,由AB为直径,根据圆周角定理得∠AFB=90°,再根据等腰三角形的性质可得∠BAF=∠EBC,从而证得BC与⊙O相切;
(2)直接利用圆周角定理求解;
(3)首先过E作EG⊥BC于点G,由三角函数的性质可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.
解答 (1)证明:连接AF,如图,
∵AB为直径,
∴∠AFB=90°,
∵AE=AB,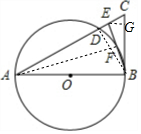
∴△ABE为等腰三角形,
∴∠BAF=$\frac{1}{2}$∠BAC.
∵∠EBC=$\frac{1}{2}$∠BAC,
∴∠BAF=∠EBC,
∴∠FAB+∠FBA=∠EBC+∠FBA=90°,即∠ABC=90°.
∴AB⊥BC,
∴BC与⊙O相切;
(2)∵AB为直径,
∴∠ADB=90°;
(3)解:过E作EG⊥BC于点G,如图,
∵∠BAF=∠EBC,
∴sin∠BAF=sin∠EBC=$\frac{1}{4}$,
在Rt△AFB中,
∴BF=AB•sin∠BAF=8×$\frac{1}{4}$=2,
∴BE=2BF=4,
在Rt△EGB中,
∴EG=BE•sin∠EBC=4×$\frac{1}{4}$=1,
∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴CE:CA=EG:AB,即CE:(CE+8)=1:8,
∴CE=$\frac{8}{7}$,
∴AC=AE+CE=8+$\frac{8}{7}$=$\frac{64}{7}$.
点评 本题考查了切线的判定与性质:经过半径的外端且垂直于这条半径的直线是圆的切线;圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了解直角三角形和利用相似比计算线段的长.

练习册系列答案
相关题目
5.下列各式计算正确的是( )
| A. | a2×a3=a6 | B. | $\sqrt{\frac{3}{2}}÷\sqrt{2}=\frac{{\sqrt{3}}}{2}$ | C. | $\frac{x-1}{{1-{x^2}}}=\frac{1}{x+1}$ | D. | (x+y)2=x2+y2 |
 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°.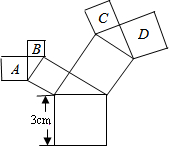 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2.