题目内容
3.将下列各式因式分解:(1)a3-4a
(2)n2(m-2)-n(2-m)
(3)b3-4b2+4b
(4)4(a+b)2-(2a-3b)2.
分析 (1)原式提取a,再利用平方差公式分解即可;
(2)原式变形后,提取公因式即可得到结果;
(3)原式提取b,再利用完全平方公式分解即可;
(4)原式利用平方差公式分解即可.
解答 解:(1)原式=a(a2-4)=a(a+2)(a-2);
(2)原式=n2(m-2)+n(m-2)=n(m-2)(n+1);
(3)原式=b(b2-4b+4)=b(b-2)2;
(4)原式=[2(a+b)+(2a-3b)][2(a+b)-(2a-3b)]=5b(4a-b).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
15.目前节能灯在城市已基本普及,为响应号召,某商场计划用3800元购进甲,乙两种节能灯共120只,这两种节能灯的进价、售价如下表:
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)全部售完120只节能灯后,该商场获利多少元?

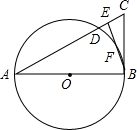 如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=$\frac{1}{2}$∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=$\frac{1}{2}$∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.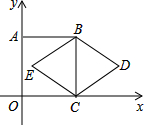 如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点E的坐标是(2-$\sqrt{3}$,1).
如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点E的坐标是(2-$\sqrt{3}$,1).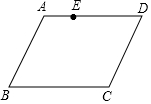 如图,点E是?ABCD边AD上一点,请你只用一把没有刻度的直尺,在BC边上确定一点F,使得CF=AE,请画出示意图,并用你学过的知识验证CF=AE.
如图,点E是?ABCD边AD上一点,请你只用一把没有刻度的直尺,在BC边上确定一点F,使得CF=AE,请画出示意图,并用你学过的知识验证CF=AE.