题目内容
6.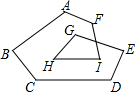 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°.
分析 根据多边形的内角和,可得答案.
解答 解:连EF,GI,如图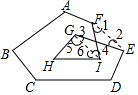 ,
,
∵6边形ABCDEFK的内角和=(6-2)×180°=720°,
∴∠A+∠B+∠C+∠D+∠E+∠F=720°-(∠1+∠2),
即∠A+∠B+∠C+∠D+∠E+∠F+(∠1+∠2)=720°,
∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F∠H+(∠3+∠4)=900°,
∴∠A+∠B+∠C+∠D+∠E+∠F(∠3+∠4)+∠5+∠6+∠H=720°+180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°,
故答案为:900°.
点评 本题考查了n边形的内角和定理:n边形的内角和为(n-2)×180°(n≥3的整数).

练习册系列答案
相关题目
15.目前节能灯在城市已基本普及,为响应号召,某商场计划用3800元购进甲,乙两种节能灯共120只,这两种节能灯的进价、售价如下表:
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)全部售完120只节能灯后,该商场获利多少元?
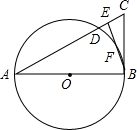 如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=$\frac{1}{2}$∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=$\frac{1}{2}$∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.