如图.在△ABC中.∠ABC和∠ACB的平分线交于点D.过点D作EF∥BC交AB于E.交AC于F.若AB=12.BC=8.AC=10.则△AEF的周长为( )A．15B．18C．20D．22 题目和参考答案——青夏教育精英家教网—

题目内容

20．

如图，在△ABC中，∠ABC和∠ACB的平分线交于点D，过点D作EF∥BC交AB于E，交AC于F，若AB=12，BC=8，AC=10，则△AEF的周长为（　　）

A．

B．

C．

D．

分析利用平行和角平分线的定义可得到∠EBD=∠EDB，所以可得ED=EB，同理可得DF=FC，所以△AEF的周长即为AB+AC，可得出答案．

解答解：∵EF∥BC，
∴∠EDB=∠DBC，
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∴∠EBD=∠EDB，
∴ED=EB，
同理可证得DF=FC，
∴AE+AF+EF=AE+EB+AF+FC=AB+AC=22，
即△AEF的周长为22，
故选D．

点评本题主要考查等腰三角形的判定和性质，由条件得到ED=EB，DF=FC是解题的关键．

练习册系列答案

考必胜小学毕业升学考试试卷精选系列答案

11．用三块正多边形的木板铺地，拼在一起并相交于一点的各边完全吻合，若其中两块木板的边数均为5，则第三块木板的边数为（　　）

8．两条直线相交于一点，则共有对顶角的对数为（　　）

15．

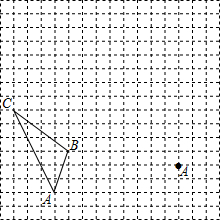如图，在边长为1个单位长度的小正方形组成的网格中，
（1）给出了格点△ABC（顶点是网格线的交点）和点A₁．画出一个格点△A₁B₁C₁，并使它与△ABC全等且A与A₁是对应点；
（2）建立平面直角坐标系，使点B的坐标为（0，-3），点C的坐标为（-4，0），请画出△ABC关于x轴对称的图形；
（3）在（2）所建立的平面直角坐标系中，在y轴上存在点D，使BC为边的△BCD是等腰三角形，则符合条件的点D共有4个．

5．已知⊙A、⊙B、⊙C的半径都是3，且相互外切．在此三个圆所在的平面上，取与这三个圆上至少一点的距离为2$\sqrt{3}$-3的所有点，试求全部取出的点所构成的区域面积．

12．

如图所示，点D、E分别在AB、AC上，F为BC上一点，延长FE交BA的延长线于G，∠EFC=∠G+∠GDE，求证：DE∥BC．

9．直线l上依次有三点A、B、C，线段AC=80cm，一只电子蚂蚁甲从C点出发向A点移动，运动速度为1cm/s．
（1）当甲走到BC中点D时，求它到A、B的距离和；
（2）当甲从BC中点D走到AB中点E共用了多长时间？
（3）当甲从AB中点E返回时，另一电子蚂蚁从C点出发，向点A移动速度为2cm/s．两只蚂蚁相遇在离B点6cm处，试求线段AB的长度．

10．

如图，DE是△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=5，BC=8，则EF的长为（　　）

试题分类