题目内容
5.已知⊙A、⊙B、⊙C的半径都是3,且相互外切.在此三个圆所在的平面上,取与这三个圆上至少一点的距离为2$\sqrt{3}$-3的所有点,试求全部取出的点所构成的区域面积.分析 由已知条件得到△ABC为正三角形,边长为6,设△ABC的中心为O,解直角三角形得到OA=OB=OC=2$\sqrt{3}$,如图,作O点关于AB,BC,CA的对称点O1,O2,O3,连接AO1,O1B,B2,O2C,CO3,O3A,于是得到所求结论.
解答 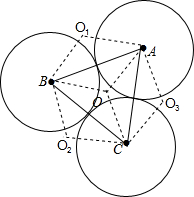 解:由题设知,△ABC为正三角形,边长为6,
解:由题设知,△ABC为正三角形,边长为6,
设△ABC的中心为O,OA=OB=OC=2$\sqrt{3}$,
如图,作O点关于AB,BC,CA的对称点O1,O2,O3,连接AO1,O1B,B2,O2C,CO3,O3A,
故所求区域为O1BO2,O2CO3,O3AO1(半径为2$\sqrt{3}$,圆心角为$\frac{4π}{3}$)
及正六边形AO1BO2CO3去掉三个圆⊙A,⊙B,⊙C(半径为6-2$\sqrt{3}$)
其面积为3×$\frac{2π}{3}$(2$\sqrt{3}$)2+6×$\frac{\sqrt{3}}{4}$(2$\sqrt{3}$)2-3π(6-2$\sqrt{3}$)2
=24π+18$\sqrt{3}$-36π(4-2$\sqrt{3}$)
=18$\sqrt{3}+π$(72$\sqrt{3}$-120).
点评 本题考查了相切两圆的性质,等边三角形的判定和性质,圆心角定义,正确的周长图形是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
15.解方程组$\left\{\begin{array}{l}{17x-2y=8①}\\{13x-4y=-10②}\end{array}\right.$时,消去未知数y最简单的方法是( )
| A. | ①×4-②×2 | B. | ①×2-② | ||
| C. | 由①得y=$\frac{17x-8}{2}$,再代入② | D. | 由②得$\frac{13x+10}{4}$,再代入① |
16.某公司经过市场调研,决定从明年起对甲、乙两种产品实行“限产压库”,要求这两种产品全年共新增产量20件,这20件的总产值p(万元)满足:1100<p<1200,已知有关数据如图所示,设生产甲种产品x件,解答下列问题:
(1)求P与x的函数关系式?
(2)该公司明年应该怎样安排甲、乙两种产品的生产量?
(3)如果甲种产品每件的成本为10万元,乙种产品每件的成本为15万元生产这两种产品的总成本为y万元,请写出y与x的函数关系式,并说明x取何值时能使总成本最低?
| 产品 | 每件产品的产值 |
| 甲 | 45万元 |
| 乙 | 75万元 |
(2)该公司明年应该怎样安排甲、乙两种产品的生产量?
(3)如果甲种产品每件的成本为10万元,乙种产品每件的成本为15万元生产这两种产品的总成本为y万元,请写出y与x的函数关系式,并说明x取何值时能使总成本最低?
 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切与F,且AB∥CD,AB=4cm,则阴影部分的面积为2πcm2.
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切与F,且AB∥CD,AB=4cm,则阴影部分的面积为2πcm2. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于F,若AB=12,BC=8,AC=10,则△AEF的周长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于F,若AB=12,BC=8,AC=10,则△AEF的周长为( ) 如图,某原形状为四边形的原材料ABCD,点E在CD上,AE∥BC,且AE=DE,∠D-∠C=27°,工人师傅将该原材料加工去一角,则被加工掉的∠D的度数为69°.
如图,某原形状为四边形的原材料ABCD,点E在CD上,AE∥BC,且AE=DE,∠D-∠C=27°,工人师傅将该原材料加工去一角,则被加工掉的∠D的度数为69°.
 如图,将?ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F.
如图,将?ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F.