题目内容
10.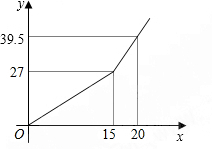 某市自来水公司为鼓励居民节约用水,采取月用水量分段收费方法.若某户居民应交水费y(元)与用水量x(方)的函数关系如图所示.
某市自来水公司为鼓励居民节约用水,采取月用水量分段收费方法.若某户居民应交水费y(元)与用水量x(方)的函数关系如图所示.(1)分别求出当0≤x≤15和x>15时,y与x的函数关系式.
(2)若某用户该月用水21方,则应交水费多少元?
(3)若小明家每月水费不少于79.5元,则小明家每月用水量不少于多少方?
分析 (1)先根据待定系数法求得直线OA和AB的解析式为y=$\frac{9}{5}$x和y=2.5x-10.5(x≥15);
(2)某用户该月用水21吨其实就是x=21,代入求解即可;
(3)由题意可得2.5x-10.5≥79.5,进而得出答案.
解答 解:(1)当0≤x≤15时,过点(0,0),(15,27)
设y=kx,
∴27=15k,
∴k=$\frac{9}{5}$,
∴y=$\frac{9}{5}$x(0≤x≤15).
当x≥15时,过点A(15,27),B(20,39.5)
设y=k1x+b
则$\left\{\begin{array}{l}{27=15{k}_{1}+b}\\{39.5=20{k}_{1}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=2.5}\\{b=-10.5}\end{array}\right.$,
∴y=2.5x-10.5(x≥15);
(2)∵x=21>15,
∴y=2.5×21-10.5=42(元);
(3)设小明家每月用水x吨,
则2.5x-10.5≥79.5,
解得:x≥36,
答:小明家每月用水量不少于36吨.
点评 此题主要考查了利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.

练习册系列答案
相关题目
20.已知一个几何体的三种视图如图所示,则该几何体是( )


| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 圆柱 |
20. 如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
 如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )| A. | y=x+10 | B. | y=-x+10 | C. | y=x+20 | D. | y=-x+20 |
 如图,正方形OABC的顶点A、C分别在坐标轴的正半轴上,点B是第一象限内直线y=$\frac{1}{2}$x+3上的一点,则点B的坐标为(6,6).
如图,正方形OABC的顶点A、C分别在坐标轴的正半轴上,点B是第一象限内直线y=$\frac{1}{2}$x+3上的一点,则点B的坐标为(6,6).
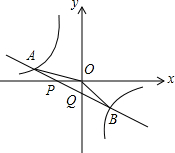 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论:
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论: 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1m),却踩伤了花草.