题目内容
1. 如图,正方形OABC的顶点A、C分别在坐标轴的正半轴上,点B是第一象限内直线y=$\frac{1}{2}$x+3上的一点,则点B的坐标为(6,6).
如图,正方形OABC的顶点A、C分别在坐标轴的正半轴上,点B是第一象限内直线y=$\frac{1}{2}$x+3上的一点,则点B的坐标为(6,6).
分析 设OA=a,根据正方形的性质可得出点B的坐标为(a,a),再利用一次函数图象上点的坐标特征即可得出a=$\frac{1}{2}$a+3,解之即可得出点B的坐标.
解答 解:∵四边形OABC为正方形,
∴OA=OC.
设OA=a,则点B的坐标为(a,a).
∵点B是第一象限内直线y=$\frac{1}{2}$x+3上的一点,
∴a=$\frac{1}{2}$a+3,解得:a=6,
∴点B的坐标为(6,6).
故答案为:(6,6).
点评 本题考查了一次函数图象上点的坐标特征以及正方形的性质,根据正方形的性质结合一次函数图象上点的坐标特征找出a=$\frac{1}{2}$a+3是解题的关键.

练习册系列答案
相关题目
11.点P1(-2,y1),点P2(3,y2)是一次函数y=-4x+m图象上的两个点,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1>y2>0 | C. | y1<y2 | D. | y1=y2 |
9.“抛一枚均匀硬币,落地后反面朝上”这一事件是( )
| A. | 随机事件 | B. | 必然事件 | C. | 确定事件 | D. | 不可能事件 |
16.解不等式组:$\left\{\begin{array}{l}{2(x-1)<3x+2}\\{\frac{x+1}{2}>x-1}\end{array}\right.$,并将解集在数轴上表示出来.
6.小亮做掷质量均为硬币的试验,掷了10次,发现有8次正面朝上,2次正面朝下,则当他第11次掷这枚硬币时( )
| A. | 一定是正面朝上 | B. | 一定是正面朝下 | ||
| C. | 正面朝上的概率为0.8 | D. | 正面朝上的概率是0.5 |
13.下列命题中:①立方根等于它本身的数有-1,0,1;②$\root{3}{6}$=2;③负数没有立方根;④内错角相等;⑤过一点有且只有一条直线和已知直线平行.正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.在△ABC中,∠C=30°,∠A与∠B的度数比是1:2,则∠A的度数是( )
| A. | 50° | B. | 100° | C. | 30° | D. | 60° |
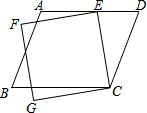 如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上,若∠ECD=35°,∠AEF=15°,则∠B的度数为70度.
如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上,若∠ECD=35°,∠AEF=15°,则∠B的度数为70度.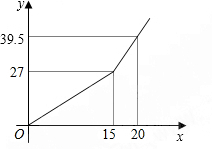 某市自来水公司为鼓励居民节约用水,采取月用水量分段收费方法.若某户居民应交水费y(元)与用水量x(方)的函数关系如图所示.
某市自来水公司为鼓励居民节约用水,采取月用水量分段收费方法.若某户居民应交水费y(元)与用水量x(方)的函数关系如图所示.