题目内容
18.等式$\sqrt{\frac{3x-1}{x-2}}$=$\frac{\sqrt{3x-1}}{\sqrt{x-2}}$成立的条件是( )| A. | x>$\frac{1}{3}$ | B. | x≥$\frac{1}{3}$ | C. | x>2 | D. | $\frac{1}{3}$≤x<2 |
分析 直接利用二次根式的性质得出关于x的不等式进而求出答案.
解答 解:∵等式$\sqrt{\frac{3x-1}{x-2}}$=$\frac{\sqrt{3x-1}}{\sqrt{x-2}}$成立,
∴$\left\{\begin{array}{l}{3x-1≥0}\\{x-2>0}\end{array}\right.$,
解得:x>2.
故选:C.
点评 此题主要考查了二次根式的性质,正确解不等式组是解题关键.

练习册系列答案
相关题目
 如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E.
如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E.
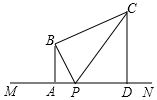 如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x 在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,求油的最大深度.
在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,求油的最大深度.