题目内容
10.若|a-7|+$\sqrt{b-24}$+(c-25)2=0,则以a、b、c为三边的三角形的形状是直角三角形.分析 根据非负数的性质列方程求出a、b、c的值,再根据勾股定理逆定理进行判断即可.
解答 解:由题意得,a-7=0,b-24=0,c-25=0,
解得a=7,b=24,c=25,
∵a2+b2=72+242=49+576=625,
c2=625,
∴a2+b2=c2,
∴以a、b、c为三边的三角形是直角三角形.
故答案为:直角三角形.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
18.等式$\sqrt{\frac{3x-1}{x-2}}$=$\frac{\sqrt{3x-1}}{\sqrt{x-2}}$成立的条件是( )
| A. | x>$\frac{1}{3}$ | B. | x≥$\frac{1}{3}$ | C. | x>2 | D. | $\frac{1}{3}$≤x<2 |
5.在实数0、-$\sqrt{7}$、|-3|、-π中,最小的是( )
| A. | -π | B. | -$\sqrt{7}$ | C. | |-3| | D. | 0 |
 如图,已知直线AB、CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,判断MQ与NP关系,并说明理由.
如图,已知直线AB、CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,判断MQ与NP关系,并说明理由.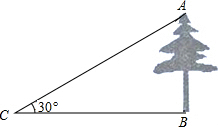 如图所示,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为30°,BC=40m,求树的高度AB.(计算过程和结果均不取近似值)
如图所示,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为30°,BC=40m,求树的高度AB.(计算过程和结果均不取近似值)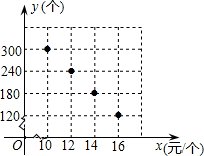 某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(单位:个)与销售单价x (单位:元/个)之间的函数关系(一次函数)如图所示:
某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(单位:个)与销售单价x (单位:元/个)之间的函数关系(一次函数)如图所示: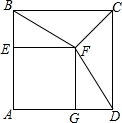 如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF、CF
如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF、CF