题目内容
7.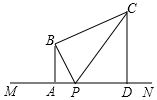 如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x(1)CD的长度是否随着的x变化而变化?若变化,请用含的x代数式表示CD的长度;若不变化,请求出线段CD的长度;
(2)当x取何值时,△ABP和△CDP相似.
分析 (1)如图1,延长CB和PA,记交点为点Q.根据等腰△QPC“三合一”的性质证得QB=BC;由相似三角形(△QAB∽△QDC)的对应边成比例得到$\frac{AB}{CD}$=$\frac{QB}{QC}$=$\frac{1}{2}$,则CD=2AB;
(2)当△BAP∽△CDP时,易得∠BPA=60°,x=AP=$\frac{BA}{tan60°}$=$\frac{4}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,当△BAP∽△PDC时,易得∠BPA=30°,AP=$\frac{BA}{tan30°}$=$\frac{4}{\frac{\sqrt{3}}{3}}$=4$\sqrt{3}$,求出x的值即可.
解答 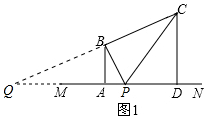 解:(1)CD的长度不变化.
解:(1)CD的长度不变化.
理由如下:
如图1,延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴$\frac{AB}{CD}$=$\frac{QB}{QC}$=$\frac{1}{2}$,
∴CD=2AB=2×4=8,
即CD=8;
(2)当△BAP∽△CDP时,
∵∠BPC=∠BPA,∠CPD=∠BPA,
∴∠BPA=∠BPC=∠CPD=60°,
∴AP=$\frac{BA}{tan60°}$=$\frac{4}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,
即x=$\frac{4\sqrt{3}}{3}$;
如图2,当△BAP∽△PDC时,
∵∠CPB=∠BPA,∠PCD=∠BPA,
∴3∠BPA=90°,
∴∠BPA=30°,
∴AP=$\frac{BA}{tan30°}$=$\frac{4}{\frac{\sqrt{3}}{3}}$=4$\sqrt{3}$,
即x=4$\sqrt{3}$;
即当x=$\frac{4\sqrt{3}}{3}$或4$\sqrt{3}$时,△ABP和△CDP相似.
点评 本题考查了相似三角形的判定与性质和锐角三角函数关系等知识,熟练利用相似三角形的性质得出线段之间的关系是解题关键.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | x>$\frac{1}{3}$ | B. | x≥$\frac{1}{3}$ | C. | x>2 | D. | $\frac{1}{3}$≤x<2 |
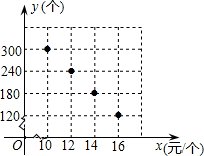 某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(单位:个)与销售单价x (单位:元/个)之间的函数关系(一次函数)如图所示:
某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(单位:个)与销售单价x (单位:元/个)之间的函数关系(一次函数)如图所示: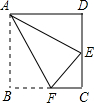 如图,将矩形ABCD沿AF折叠,点B落在CD边的中点E处,则图中等于60°的角(包括虚线)共有( )个.
如图,将矩形ABCD沿AF折叠,点B落在CD边的中点E处,则图中等于60°的角(包括虚线)共有( )个.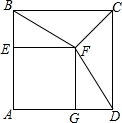 如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF、CF
如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF、CF