题目内容
8. 在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,求油的最大深度.
在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,求油的最大深度.
分析 连接OA,过点O作OE⊥AB,交AB于点M,由垂径定理求出AM的长,再根据勾股定理求出OM的长,进而可得出ME的长.
解答  解:连接OA,过点O作OE⊥AB,交AB于点M,
解:连接OA,过点O作OE⊥AB,交AB于点M,
∵直径为200cm,AB=160cm,
∴OA=OE=100cm,AM=80cm,
∴OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\sqrt{10{0}^{2}-8{0}^{2}}$=60cm,
∴ME=OE-OM=100-60=40cm.
点评 本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
18.等式$\sqrt{\frac{3x-1}{x-2}}$=$\frac{\sqrt{3x-1}}{\sqrt{x-2}}$成立的条件是( )
| A. | x>$\frac{1}{3}$ | B. | x≥$\frac{1}{3}$ | C. | x>2 | D. | $\frac{1}{3}$≤x<2 |
13.一个正多边形的每个外角都是60°,那么它是( )
| A. | 正六边形 | B. | 正七边形 | C. | 正八边形 | D. | 正九边形 |
18.下列命题中的真命题是( )
| A. | 长度相等的弧是等弧 | B. | 相似三角形的面积比等于相似比 | ||
| C. | 正方形不是中心对称图形 | D. | 圆内接四边形的对角互补 |
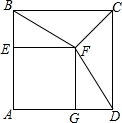 如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF、CF
如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF、CF