题目内容
18．通分：$\frac{1}{a+2b}$，$\frac{5}{a-2b}$的最简公分母是（a+2b）（a-2b），则$\frac{1}{a+2b}$=$\frac{M}{{a}^{2}-4{b}^{2}}$，$\frac{5}{a-2b}$=$\frac{N}{{a}^{2}-4{b}^{2}}$，其中M=a-2b，N=5（a+2b）．分析 利用分式的基本性质即可求出答案．
解答 解：$\frac{1}{a+2b}$，$\frac{5}{a-2b}$的最简公分母是（a+2b）（a-2b）；
∵$\frac{1}{a+2b}$=$\frac{M}{{a}^{2}-4{b}^{2}}$，$\frac{5}{a-2b}$=$\frac{N}{{a}^{2}-4{b}^{2}}$，
∴$\frac{1}{a+2b}=\frac{M}{（a+2b）（a-2b）}$，$\frac{5}{a-2b}=\frac{N}{（a-2b）（a+2b）}$，
∴M=a-2b，N=5（a+2b），
故答案为：（a+2b）（a-2b）；a-2b；5（a+2b）；
点评 本题考查分式的基本性质，涉及平方差公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
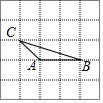如图，由25个同样大小的小正方形组成的正方形网格中，△ABC是格点三角形（每个顶点都是格点），在这个正方形网格中画另一个格点三角形，使得它与△ABC全等且仅有一条公共边，则符合要求的三角形共能画（ ）
如图，由25个同样大小的小正方形组成的正方形网格中，△ABC是格点三角形（每个顶点都是格点），在这个正方形网格中画另一个格点三角形，使得它与△ABC全等且仅有一条公共边，则符合要求的三角形共能画（ ）| A． | 5个 | B． | 6个 | C． | 7个 | D． | 8个 |
9．利用图象求得方程x2-x-1=0的近似根为（ ）
| A． | x1=1.6，x2=0.6 | B． | x1=-1.6，x2=0.6 | C． | x1=1.6，x2=-0.6 | D． | x1=-1.6，x2=-0.6 |
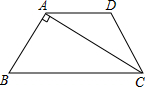如图，在四边形ABCD中，AD∥BC，AC⊥AB，AD=CD，tan∠DCA=$\frac{3}{4}$，AC=8，则AB的值是6．
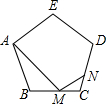如图，点M为正五边形ABCDE的边BC上一点，$\frac{BM}{CM}$=2，连结AM，作∠AMN=108°，MN交CD于点N，则$\frac{CN}{ND}$的值为$\frac{2}{7}$．
10．对于一个一次函数，x每增加1，y的值就减少2，且它的图象经过（0，3）点，则该函数的表达式为（ ）
| A． | y=2x+3 | B． | y=2x-3 | C． | y=-2x+3 | D． | y=-2x-3 |