题目内容
15. 如图,已知AD平分∠BAC,BD⊥AD于D,ED∥AC,∠BAD=36°,求∠BDE的度数.
如图,已知AD平分∠BAC,BD⊥AD于D,ED∥AC,∠BAD=36°,求∠BDE的度数.
分析 延长BD交AC于F,由角平分线得出∠FAD=∠BAD=36°,由三角形的外角性质得出∠BFC=∠FAD+∠ADF═126°,再由平行线的性质得出同位角相等即可.
解答 解:延长BD交AC于F,如图所示: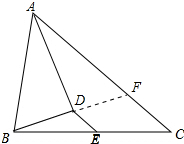
∵AD平分∠BAC,
∴∠FAD=∠BAD=36°,
∵BD⊥AD,
∴∠ADF=90°,
∴∠BFC=∠FAD+∠ADF=36°+90°=126°,
∵ED∥AC,
∴∠BDE=∠BFC=126°.
点评 本题考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质,由三角形的外角性质求出∠BFC的度数是解决问题的关键.

练习册系列答案
相关题目
5.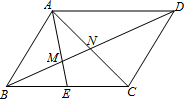 如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )
如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )
 如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )
如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 以上都不正确 |
3.乐山武警射击选拔赛中,武警战士小张和小王的总成绩相同,小张射击成绩的方差为1.247,小王射击成绩的方差为1.647,下列说法正确的是( )
| A. | 小张的方差小,射击水平没有小王稳定 | |
| B. | 小张的方差小,射击水平比小王稳定 | |
| C. | 小王的方差大,射击水平比小张稳定 | |
| D. | 两人总成绩相同,小张和小王射击稳定性相同 |
3.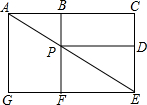 如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
 如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
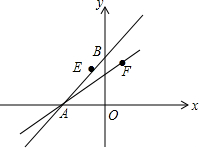 如图,直线y=x+4与x轴交于点A,与y轴交于点B,点E(-1,m)在直线y=x+4上,作点E关于y轴的对称点F,直线AF交y轴于点C.
如图,直线y=x+4与x轴交于点A,与y轴交于点B,点E(-1,m)在直线y=x+4上,作点E关于y轴的对称点F,直线AF交y轴于点C. 如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.
如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.