题目内容
4.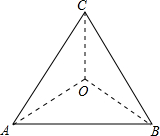 如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.
如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.
分析 由已知条件得到点O是△ABC的三边垂直平分线的交点,推出点O是△ABC的外心,延长CO交AB点D,根据勾股定理得到AD=$\sqrt{C{A}^{2}-A{D}^{2}}$=$\frac{3}{2}$$\sqrt{3}$,由重心定理即可得到结论.
解答 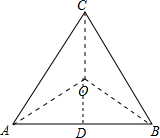 解::∵点O到△ABC的三个顶点的距离相等,
解::∵点O到△ABC的三个顶点的距离相等,
∴点O是△ABC的三边垂直平分线的交点,
∵三角形三边垂直平分线的交点是三角形的外心,
∴点O是△ABC的外心,
延长CO交AB点D,
∴AD=$\frac{1}{2}$AB=$\frac{3}{2}$,∴CD=$\sqrt{C{A}^{2}-A{D}^{2}}$=$\frac{3}{2}$$\sqrt{3}$
由重心定理得:OA=CO=$\frac{2}{3}$CD=$\sqrt{3}$,
故答案为$\sqrt{3}$.
点评 本题考查了等边三角形的性质,三角形的外心的性质,重心定理,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
16.下面各图象不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
13.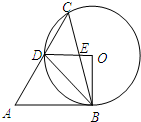 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )| A. | ∠BOD=90° | B. | DO∥AB | C. | CD=AD | D. | △BDE∽△BCD |
 如图,已知AD平分∠BAC,BD⊥AD于D,ED∥AC,∠BAD=36°,求∠BDE的度数.
如图,已知AD平分∠BAC,BD⊥AD于D,ED∥AC,∠BAD=36°,求∠BDE的度数.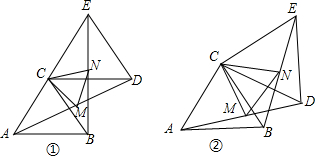
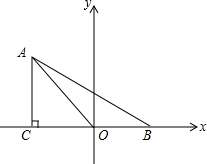 如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).
如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).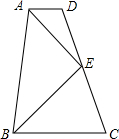 如图,在梯形ABCD中,AD∥BC,E为CD的中点,AD+BC=AB.则:
如图,在梯形ABCD中,AD∥BC,E为CD的中点,AD+BC=AB.则: