题目内容
正三角形的边长为2
cm,则它的外接圆的面积为 ,内切圆的半径是 .
| 3 |
考点:正多边形和圆
专题:
分析:根据O为等边△ABC的内心(也是等边△ABC的外心),连接OA、OC、OB,设AO交BC于D,则AD⊥BC,BD=DC,即OB是△ABC外接圆的半径,OD是△ABC内切圆的半径,求出BD=DC=
,求出∠OBD=
∠ABC=
×60°=30°,在Rt△OBD中,求出OD=BD•tan30°=1,根据OB=2OD求出OB即可得出外接圆面积.
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: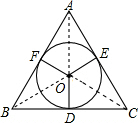 解:设O为等边△ABC的内心(也是等边△ABC的外心),连接OA、OC、OB,设AO交BC于D,
解:设O为等边△ABC的内心(也是等边△ABC的外心),连接OA、OC、OB,设AO交BC于D,
则AD⊥BC,BD=DC,
即OB是△ABC外接圆的半径,OD是△ABC内切圆的半径,
∵BC=2
,
∴BD=DC=3,
∵O为等边△ABC内切圆的圆心,
∴∠OBD=
∠ABC=
×60°=30°,
在Rt△OBD中,OD=BD•tan30°=
×
=1;
∴OB=2OD=2,
外接圆面积是4πcm2,
∴正三角形的内切圆半径是1,外接圆面积是4πcm2.
故答案为4πcm2,1cm.
 解:设O为等边△ABC的内心(也是等边△ABC的外心),连接OA、OC、OB,设AO交BC于D,
解:设O为等边△ABC的内心(也是等边△ABC的外心),连接OA、OC、OB,设AO交BC于D,则AD⊥BC,BD=DC,
即OB是△ABC外接圆的半径,OD是△ABC内切圆的半径,
∵BC=2
| 3 |
∴BD=DC=3,
∵O为等边△ABC内切圆的圆心,
∴∠OBD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OBD中,OD=BD•tan30°=
| 3 |
| ||
| 3 |
∴OB=2OD=2,
外接圆面积是4πcm2,
∴正三角形的内切圆半径是1,外接圆面积是4πcm2.
故答案为4πcm2,1cm.
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+2 |
| C、y=(x-1)2-2 |
| D、y=(x+1)2-2 |
 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. 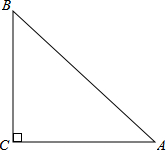 如图所示,工厂里有一个腰长为2m的等腰直角三角形余料,先从中要截下一个半圆,半圆的直径要在三角形的一条边上,且与另两边相切,请你设计裁截方案,画出示意图,并计算出半圆的半径.
如图所示,工厂里有一个腰长为2m的等腰直角三角形余料,先从中要截下一个半圆,半圆的直径要在三角形的一条边上,且与另两边相切,请你设计裁截方案,画出示意图,并计算出半圆的半径. 如图,a个半圆弧依次相外切,他们的圆心都在x轴的正半轴上,并都与直线y=
如图,a个半圆弧依次相外切,他们的圆心都在x轴的正半轴上,并都与直线y= 如图是西安交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时).
如图是西安交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时).