题目内容
 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. (1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若∠BEC=30°,求证:以BC,BE,AC边的三角形为直角三角形.
考点:切线的性质
专题:
分析:(1)连接OC,可证得OC∥AD,结合条件可证得∠DAC=∠CAB,可证得结论;
(2)由条件可得∠BCP=∠CAB,∠BCF=∠ACF,结合外角性质可得∠PCF=∠PFC,可证得结论;
(3)连接AE,可知BE=AE,根据条件可得到BE与AB的关系,以及BC、AC和AB的关系,再结合勾股定理的逆定理可得到结论.
(2)由条件可得∠BCP=∠CAB,∠BCF=∠ACF,结合外角性质可得∠PCF=∠PFC,可证得结论;
(3)连接AE,可知BE=AE,根据条件可得到BE与AB的关系,以及BC、AC和AB的关系,再结合勾股定理的逆定理可得到结论.
解答:证明:(1)如图1,连接OC,

∵DP是⊙O的切线,
∴OC⊥DP,
又∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
(2)∵PD是⊙O的切线,
∴∠BCP=∠CAB,
又∵CE平分∠ACB,
∴∠ACF=∠BCF,
∴∠CAF+∠ACF=∠BCF+∠PCB,
即∠CFP=∠PCF,
∴PC=PF,即△PCB为等腰三角形;
(2)如图2,连接AE,

∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴AE=BE,
又∵AB为直径,
∴BE=
AB,
∵∠CEB=30°,
∴∠CAB=30°,
∴在Rt△ABC中,BC=
AB,AC=
AB,
∴BC2+BE2=
AB2=AC2,
∴以BC,BE,AC边的三角形为直角三角形.

∵DP是⊙O的切线,
∴OC⊥DP,
又∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
(2)∵PD是⊙O的切线,
∴∠BCP=∠CAB,
又∵CE平分∠ACB,
∴∠ACF=∠BCF,
∴∠CAF+∠ACF=∠BCF+∠PCB,
即∠CFP=∠PCF,
∴PC=PF,即△PCB为等腰三角形;
(2)如图2,连接AE,

∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴AE=BE,
又∵AB为直径,
∴BE=
| ||
| 2 |
∵∠CEB=30°,
∴∠CAB=30°,
∴在Rt△ABC中,BC=
| 1 |
| 2 |
| ||
| 2 |
∴BC2+BE2=
| 3 |
| 4 |
∴以BC,BE,AC边的三角形为直角三角形.
点评:本题主要考查切线的性质和等腰三角形的判定及勾股定理的逆定理,在(1)中根据平行得到角之间的关系是解题的关键,在(2)中注意弦切角定理的应用,在(3)中用AB分别表示出BE、BC、AC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.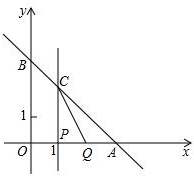 已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒.
已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒. 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4cm,将腰CD以D为中心逆时针旋转90°至DE,连结AE、CE,若△ADE的面积是6cm2,则BC=
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4cm,将腰CD以D为中心逆时针旋转90°至DE,连结AE、CE,若△ADE的面积是6cm2,则BC=