题目内容
16.在正方形ABCD中,点H在对角线BD上(与点B、D不重合),连接AH,将HA绕点H顺时针旋转90°与边CD(或CD延长线)交于点P,作HQ⊥BD交射线DC于点Q.(1)如图1:
①依题意补全图1;
②判断DP与CQ的数量关系并加以证明;
(2)若正方形ABCD的边长为$\sqrt{3}$,当 DP=1时,试求∠PHQ的度数.

分析 (1)①由题意画出图形即可,②先由旋转得出∠AHP=90°,然后判断出∠QHP=AHD,再得出△QHP≌△DHA即可;
(2)分两种情况计算,先由三角函数求出∠APD=60°,再求出∠APH=45°,最后得到∠PHQ=60°即可.
解答 解:(1)①依题意,补全图形,如图1所示,
②DP=CQ,
∵HA绕点H顺时针旋转90°,与边CD(或CD延长线)相交于点P,
∴∠AHP=90°,
∴∠AHD+DHP=90°,
∵HQ⊥BD,
∴∠QHD=90°,
∴∠QHP+∠DHP=90°,
∴∠QHP=AHD,
∵四边形ABCD为正方形,
∴∠CDB=∠ADB=45°,AD=CD,
∴∠Q=∠CDB=∠ADB=45°,
∴△QHP≌△DHA,
∴AD=QP,
∴QP=CD,
∴OP-PC=CD-PC,
∴CQ=PD;
(2)①如图2,当点P在边CD上时,连接AP,
∵正方形的边长为$\sqrt{3}$,PD=1,∠ADP=90°,
∴tan∠APD=$\sqrt{3}$,
∴∠APD=60°,
∵HA=HP,∠AHP=90°,
∴∠APH=45°,
∴∠HPD=∠APH+∠APD=105°,
∵∠Q=45°,
∴∠PHQ=60°,
②如图3,当点P在边CD的延长线时,连接AP,
∴∠HPD=∠APD-∠APH=15°,
∵∠HQD=45°,
∴∠PHQ=120°,
∴∠PHQ的度数为120°或60°.
点评 此题是四边形综合题,主要考查了正方形的性质和旋转的特征,全等三角形的判定和性质,同角或等角的余角相等,判断△QHP≌△DHA是解本题的关键,分两种情况是解本题的难点.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
7.下列计算中正确的是( )
| A. | x6÷x2=x3 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | $\sqrt{18}$×$\sqrt{2}$=6 | D. | (a-2)2=a2-2a+4 |
1.下列计算正确的是( )
| A. | x3•x3=2x3 | B. | 4${\;}^{-2}=\frac{1}{16}$ | C. | $\sqrt{9}=±3$ | D. | (x3)2=x5 |
 已知菱形ABCD,AB=4,∠B=60°,以点D为圆心作⊙D与直线AB相切于点G,连接DG.
已知菱形ABCD,AB=4,∠B=60°,以点D为圆心作⊙D与直线AB相切于点G,连接DG. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: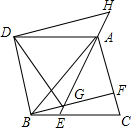 如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.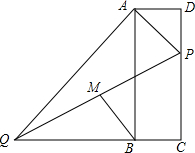 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.