题目内容
13.(1)计算:$\frac{a+b}{ab}$-$\frac{b+c}{bc}$(2)计算:($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$.
分析 (1)先通分,再把分子相加减即可;
(2)先算括号里面的,再算除法即可.
解答 解:(1)原式=$\frac{c(a+b)}{abc}$-$\frac{a(b+c)}{abc}$
=$\frac{ac+bc-ab-ac}{abc}$
=$\frac{bc-ab}{abc}$
=$\frac{c-a}{ac}$;
(2)原式=$\frac{a-(a-b)}{(a+b)(a-b)}$•$\frac{b-a}{b}$
=$\frac{b}{(a+b)(a-b)}$•$\frac{b-a}{b}$
=-$\frac{1}{a+b}$.
点评 本题考查的是分式的混合运算,分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列式子:①-7<0;②3x+1>0;③x≥2;④x-6.其中,是不等式的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
1.如果a>b,那么下列不等式中一定成立的是( )
| A. | a2>b2 | B. | 1-a>1-b | C. | 1+a>1-b | D. | 1+a>b-1 |
8.下表是截至到2002年菲尔兹奖得主获奖时的年龄:
根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄.
| 年龄 | 28≤X<30 | 30≤X<32 | 32≤X<34 | 34≤X<36 | 36≤X<38 | 38≤X<40 | 40≤X<42 |
| 频数 | 4 | 3 | 8 | 7 | 9 | 11 | 2 |
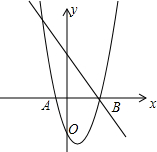 如图,抛物线y=x2-2x-3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=$\frac{4}{3}$,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是$\frac{64}{9}$s.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=$\frac{4}{3}$,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是$\frac{64}{9}$s.