题目内容
3.解方程组:(1)$\left\{\begin{array}{l}{2x-y=0}\\{3x-2y=5}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y+1}{3}=1}\\{3x+2y=10}\end{array}\right.$.
分析 (1)先用加减消元法求出x的值,再用代入消元法求出y的值即可;
(2)先把方程组中的方程化为不含分母及括号的方程,再用加减消元法或代入消元法求解即可.
解答 解:(1)$\left\{\begin{array}{l}2x-y=0①\\ 3x-2y=5②\end{array}\right.$,①×2-②得,x=-5,把x=-5代入①得,-10-y=0,解得y=-10,
故方程组的解为$\left\{\begin{array}{l}x=-5\\ y=-10\end{array}\right.$;
(2)原方程组可化为$\left\{\begin{array}{l}3x-2y=8①\\ 3x+2y=10②\end{array}\right.$,①+②得,6x=18,解得x=3,把x=3代入①得,9-2y=8,解得y=$\frac{1}{2}$,
故方程组的解为$\left\{\begin{array}{l}x=3\\ y=\frac{1}{2}\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列数学表达式中,①-8<0;②4a+3b>0;③a=3;④a+2>b+3,不等式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
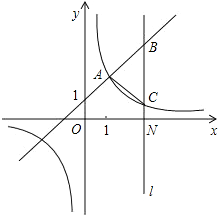 如图,一次函数y=kx+1(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象有公共点A(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别相交于B,C,连接AC.
如图,一次函数y=kx+1(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象有公共点A(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别相交于B,C,连接AC. 如图,点P为?ABCD的对角线BD上任意一点,猜想S△BPC和S△ABP的大小关系.并说明理由.
如图,点P为?ABCD的对角线BD上任意一点,猜想S△BPC和S△ABP的大小关系.并说明理由.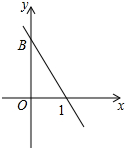 如图,在平面直角坐标系xOy中,直线$y=-\frac{3}{2}x+b$经过第一、二、四象限,与y轴交于点B,点A(2,m)在这条直线上,连结AO,△AOB的面积等于2.
如图,在平面直角坐标系xOy中,直线$y=-\frac{3}{2}x+b$经过第一、二、四象限,与y轴交于点B,点A(2,m)在这条直线上,连结AO,△AOB的面积等于2.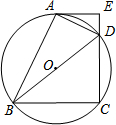 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.