题目内容
17.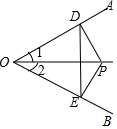 如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )| A. | PD=PE | B. | OP平分∠DPE | C. | OD=OE | D. | DE垂直平分OP |
分析 由已知条件认真思考,首先可得△POE≌△POD,进而可得PD=PE,∠1=∠2,∠DPO=∠EPO;而OD,OP是无法证明是相等的,于是答案可得.
解答 解:∵∠POB=∠POA,PD⊥OA,PE⊥OB,
∴PE=PD,
∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°,
∵OP=OP,PE=PD,
∴由勾股定理得:OE=OD,
∵∠PEO=∠PDO=90°,∠POB=∠POA,
∴由三角形的内角和定理得:∠DPO=∠EPO,
∴OP平分∠DPE,
根据已知不能推出PD=OD,OD=OE,
∴OP垂直平分DE;
故选D.
点评 本题考查了线段垂直平分线性质,角平分线性质,全等三角形的性质和判定的应用,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
7.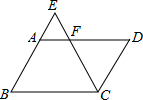 如图,E是?ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
如图,E是?ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
 如图,E是?ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
如图,E是?ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )| A. | $\frac{AE}{BE}$=$\frac{AF}{BC}$ | B. | $\frac{AE}{AB}$=$\frac{AF}{DF}$ | C. | $\frac{AE}{AB}$=$\frac{FE}{FC}$ | D. | $\frac{AE}{AB}$=$\frac{AF}{BC}$ |
5. 如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )
如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )
 如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )
如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )| A. | 70° | B. | 60° | C. | 55° | D. | 35° |
9.等腰三角形一个底角为80°,则它的顶角的度数是( )
| A. | 80° | B. | 50° | C. | 80°或20° | D. | D20° |
6.若a<$\sqrt{11}$<b,且a,b为两个连续的正整数,则a+b等于( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
7.按一定规律排列的一组数:3,5,9,17,33,…,第2017个数是( )
| A. | 22017-1 | B. | 22017+1 | C. | 22016-1 | D. | 22016+1 |
 如图,直线l与⊙O相切于点A,AC为⊙O的直径,AC=8,P是直径AC右侧半圆上的一个动点(不与点A、C重合),过点P作PB⊥l,垂足为B,连接PA、PC.设PA=x,PB=y.求:
如图,直线l与⊙O相切于点A,AC为⊙O的直径,AC=8,P是直径AC右侧半圆上的一个动点(不与点A、C重合),过点P作PB⊥l,垂足为B,连接PA、PC.设PA=x,PB=y.求: 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B($\frac{1}{2}$,y2),点C($\frac{5}{2}$,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B($\frac{1}{2}$,y2),点C($\frac{5}{2}$,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( ) (一)知识拓展
(一)知识拓展