题目内容
7.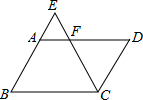 如图,E是?ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
如图,E是?ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是( )| A. | $\frac{AE}{BE}$=$\frac{AF}{BC}$ | B. | $\frac{AE}{AB}$=$\frac{AF}{DF}$ | C. | $\frac{AE}{AB}$=$\frac{FE}{FC}$ | D. | $\frac{AE}{AB}$=$\frac{AF}{BC}$ |
分析 由平行四边形的性质可知:AF∥BC,AE∥CD,由此可知:△AEF∽△BEC、△AEF∽△DCF,由相似三角形的性质即可判定.
解答 解:由平行四边形的性质可知:AF∥BC,
∴△AEF∽△BEC
∴$\frac{AE}{BE}=\frac{AF}{BC}$,$\frac{AE}{AB}=\frac{FE}{FC}$,故A、C正确,
由平行四边形的性质可知:AE∥CD,AB=CD,
∴△AEF∽△DCF,
∴$\frac{AE}{CD}=\frac{AF}{DF}$,
∴$\frac{AE}{AB}=\frac{AF}{DF}$,故B正确,
故选(D)
点评 本题考查相似三角形的判定与性质,涉及平行四边形的性质,题目较为综合.

练习册系列答案
相关题目
18.在0,|-5|,-(-2),-32各数中,负数的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
2. 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )| A. | 4 | B. | 8 | C. | 10 | D. | 6 |
12.将抛物线y=x2向右平移两个单位,再向下平移4个单位,所得抛物线是( )
| A. | y=(x+2)2+4 | B. | y=(x-2)2-4 | C. | y=(x-2)2+4 | D. | y=(x+2)2-4 |
19. 若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
 若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )| A. | a+b>0 | B. | a-b<0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
16.计算:a•a2的结果是( )
| A. | 3a | B. | a3 | C. | 2a2 | D. | 2a3 |
17.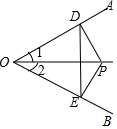 如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
 如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )| A. | PD=PE | B. | OP平分∠DPE | C. | OD=OE | D. | DE垂直平分OP |