题目内容
5. 如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )
如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )| A. | 70° | B. | 60° | C. | 55° | D. | 35° |
分析 由AD为圆的切线,利用切线的性质得到AD与AC垂直,根据弧AB的度数求出所对圆心角的度数,进而∠C的度数,在直角三角形中求出所求角度数即可.
解答 解:∵AD是⊙O的切线,切点为A,AC是⊙O的直径,
∴AD⊥AC,即∠A=90°,
∵$\widehat{AB}$的度数为70°,
∴∠AOB=70°,
∵∠C与∠AOB都对$\widehat{AB}$,
∴∠C=$\frac{1}{2}$∠AOB=35°,
在Rt△ACD中,∠C=35°,
∴∠D=55°,
故选C
点评 此题考查了切线的性质,圆周角定理,以及弧、圆心角、圆周角之间的关系,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
16.计算:a•a2的结果是( )
| A. | 3a | B. | a3 | C. | 2a2 | D. | 2a3 |
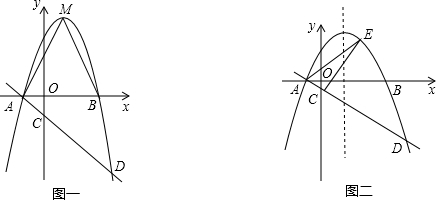
20.已知二次函数y=ax2+bx+c中,y与x的部分对应值如表所示,则下列结论错误的是( )
| x | … | -1 | 1 | 2 | 3 | 4 | … |
| y | … | -5 | 3 | 4 | 3 | 0 | … |
| A. | 抛物线开口向下 | |
| B. | 二次函数y=ax2+bx+c的最大值为4 | |
| C. | 当x=5时,y<0 | |
| D. | 一元二次方程ax2+bx+c=0的两个根均为正数 |
17.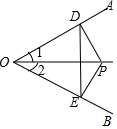 如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
 如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )| A. | PD=PE | B. | OP平分∠DPE | C. | OD=OE | D. | DE垂直平分OP |
14.抛物线y=2(x-3)2-1的顶点坐标是( )
| A. | (3,1) | B. | (3,-1) | C. | (-3,1) | D. | (-3,-1) |
15.若$\frac{a}{b}$=$\frac{1}{2}$,则$\frac{a}{a+b}$的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
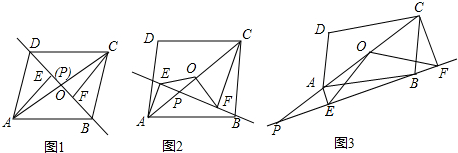
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )