题目内容
7.一个圆被分成四个扇形,若各个扇形的面积之比为4:2:1:3,则最小的扇形的圆心角的度数为36°.分析 因为扇形A,B,C,D的面积之比为4:2:1:3,所以其所占扇形比分别为:$\frac{4}{10},\frac{2}{10},\frac{1}{10},\frac{3}{10}$,则最小扇形的圆心角度数可求.
解答 解:∵扇形A,B,C,D的面积之比为4:2:1:3,
∴其所占扇形比分别为:$\frac{4}{10},\frac{2}{10},\frac{1}{10},\frac{3}{10}$,
∴最小的扇形的圆心角是360°×$\frac{1}{10}$=36°.
故答案为:36°.
点评 本题考查扇形统计图及相关计算,要求同学们掌握圆心角的度数=360°×该部分占总体的百分比.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 零表示什么也没有 | |
| B. | 1没有符号 | |
| C. | 零既然不是正数,那是负数 | |
| D. | 一场比赛赢3个球得+3分,-2分表示输了2个球 |
 如图所示,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,∠ADB=100°,则∠BAC的度数是50°.
如图所示,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,∠ADB=100°,则∠BAC的度数是50°.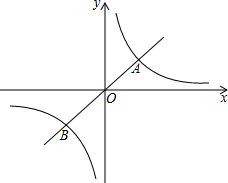 若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B.
若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B. 如图所示是长方体的表面展开图,折叠成一个长方体.
如图所示是长方体的表面展开图,折叠成一个长方体.