题目内容
2.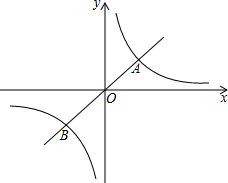 若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B.
若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B.(1)求点A和点B的坐标;
(2)求正比例函数y=mx的解析式;
(3)C(1,n)为反比例函数上一点,求△AOC的面积.
分析 (1)把A的坐标代入反比例函数的解析式求出a的值,根据中心对称图形的性质可得B的坐标;
(2)先把A的坐标代入y=mx,利用待定系数法求出正比例函数y=mx的解析式;
(3)把C的坐标代入反比例函数的解析式求出n的值,求出点C的坐标,过A点作AE⊥y轴,过C点作CF⊥y轴,进而根据△AOC的面积=梯形CFEA的面积+△AOE的面积-△COF的面积,列式计算即可求解.
解答 解:(1)∵反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2),
∴2=$\frac{6}{a}$,解得a=3.
故点A(3,2),
∴点B(-3,-2);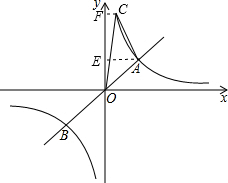 (2)∵反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(3,2),
(2)∵反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(3,2),
∴2=3m,解得m=$\frac{2}{3}$.
故正比例函数y=$\frac{2}{3}$x的解析式;
(3)∵C(1,n)为反比例函数上一点,
∴n=$\frac{6}{1}$=6,
∴C(1,6),
过A点作AE⊥y轴,过C点作CF⊥y轴,
则△AOC的面积=梯形CFEA的面积+△AOE的面积-△COF的面积
=$\frac{1}{2}$×(1+3)×(6-2)+3-3
=8.
故△AOC的面积是8.
点评 本题考查了用待定系数法求一次函数的解析式,一次函数与反比例函数图象上点的坐标特征,三角形的面积,一次函数与反比例函数的交点问题的应用,数形结合思想的应用,主要考查学生运用性质进行计算的能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
12.下列方程有实数根的是( )
| A. | x2+10=0 | B. | x2+x+1=0 | C. | x2-x-1=0 | D. | x2-$\sqrt{2}$x+1=0 |
14.下列一元二次方程中,有两个不相等的实数根的方程是( )
| A. | x2=4x-4 | B. | x2+2x=-3 | C. | x2-3x-1=0 | D. | x2+1=0 |
12.若分式$\frac{3}{(x-1)(x+2)}$有意义,则x的取值范围是( )
| A. | x≠0 | B. | x≠1且x≠-2 | C. | x≠-1或x≠-2 | D. | x=1且x=-2 |