题目内容
14.(1)已知a-b=2$\sqrt{3}$-1,ab=$\sqrt{3}$,求(a+1)(b-1)的值(2)计算:$\frac{3\sqrt{2}}{\sqrt{2}-\sqrt{3}}$-$\frac{2\sqrt{3}+3}{\sqrt{3}+2}$+$\frac{\sqrt{18}}{\sqrt{3}-\sqrt{2}}$.
分析 (1)先将所求的式子展开,然后将a-b=2$\sqrt{3}$-1,ab=$\sqrt{3}$代入即可解答本题;
(2)先化简,然后根据二次根式的加法和减法即可解答本题.
解答 解:(1)∵a-b=2$\sqrt{3}$-1,ab=$\sqrt{3}$,
∴(a+1)(b-1)
=ab-a+b-1
=ab-(a-b)-1
=$\sqrt{3}$-($2\sqrt{3}-1$)-1
=$\sqrt{3}-2\sqrt{3}+1-1$
=$-\sqrt{3}$;
(2)$\frac{3\sqrt{2}}{\sqrt{2}-\sqrt{3}}$-$\frac{2\sqrt{3}+3}{\sqrt{3}+2}$+$\frac{\sqrt{18}}{\sqrt{3}-\sqrt{2}}$
=$\frac{3\sqrt{2}}{\sqrt{2}-\sqrt{3}}-\frac{(2\sqrt{3}+3)(\sqrt{3}-2)}{(\sqrt{3}+2)(\sqrt{3}-2)}-\frac{3\sqrt{2}}{\sqrt{2}-\sqrt{3}}$
=$(\frac{3\sqrt{2}}{\sqrt{2}-\sqrt{3}}-\frac{3\sqrt{2}}{\sqrt{2}-\sqrt{3}})-\frac{-\sqrt{3}}{-1}$
=0-$\sqrt{3}$
=-$\sqrt{3}$.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.

练习册系列答案
相关题目
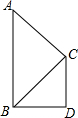 如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长.
如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长. 用一段长为36米的篱笆围成一个一边靠墙的矩形菜园,墙长为18米
用一段长为36米的篱笆围成一个一边靠墙的矩形菜园,墙长为18米