题目内容
19．
用一段长为36米的篱笆围成一个一边靠墙的矩形菜园，墙长为18米（1）若围成的面积为160米2，求矩形的长与宽；
（2）若使围成的面积最大，此时这个矩形菜园长、宽各为多少米？最大面积是多少？
分析 （1）设AB=x米，则BC=（30-2x）米，根据菜园ABCD的面积为160平方米，列方程求解，然后由墙长为18m检验即可；
（1）设菜园的面积为S，由面积公式写出S与x的函数关系式，利用二次函数求最值的知识可得出菜园的最大面积．
解答 解：（1）设与墙垂直的边长为x米，则与墙平行的边长为（36-2x）米．
根据题意得：x（36-2x）=160，
解得：x1=8，x2=10．
当x=8米时，36-2x=36-16=20米＞18米（不合题意，舍去）；
当x=10米时，36-2x=36-20=16米＜18米符合题意．
∴矩形的长为16米，宽为10米；
（2）设矩形的面积为S，
由题意得：S=x（36-2x）=-2x2+36x（0＜x≤18）；
∵S=-2x2+36x=-2（x-9）2+162，
∴当x=9时，S有最大值，S最大=162，36-2x=18，
此时这个矩形的长为18米，宽为9米，菜园的面积最大，最大面积是162平方米．
点评 此题主要考查了二次函数的应用，难度一般，应注意配方法求最大值在实际中的应用．
练习册系列答案
相关题目
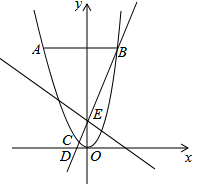如图，A、B分别为y=x2上两点，线段AB⊥y轴，且AB=2+2$\sqrt{3}$，过B的直线l：y=kx+b与抛物线交于点C（1-$\sqrt{3}$，m），与x轴、y轴交于D、E两点．