题目内容
6.计算①$\frac{a-2}{a+3}$÷$\frac{{{a^2}-4}}{{{a^2}+6a+9}}$.
②$\frac{{{x^2}-8x+16}}{{4-{x^2}}}$÷$\frac{{16-{x^2}}}{{4+4x+{x^2}}}$.
分析 ①先对分子分母因式分解,再约分即可;
②先对分子分母因式分解,再约分即可.
解答 解:①原式=$\frac{a-2}{a+3}$•$\frac{(a+3)^{2}}{(a+2)(a-2)}$
=$\frac{a+3}{a+2}$;
②原式=$\frac{(x-4)^{2}}{-(x+2)(x-2)}$•$\frac{(x+2)^{2}}{-(x+4)(x-4)}$
=$\frac{(x-4)(x+2)}{(x-2)(x+4)}$
=$\frac{{x}^{2}-2x-8}{{x}^{2}+2x-8}$.
点评 本题考查了分式的乘除法,掌握因式分解是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
19.下列各数-2,3,0.75,-5.4,|-9|,-3,0,4中,属于整数的有___个,属于有理数的有___个( )
| A. | 6,4 | B. | 5,5 | C. | 4,3 | D. | 6,8 |
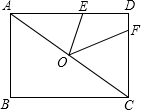 如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO.
如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO.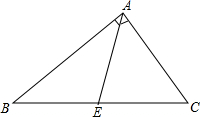 如图,已知AE是△ABC的中线,AB=8cm,AC=6cm,∠CAB=90°.
如图,已知AE是△ABC的中线,AB=8cm,AC=6cm,∠CAB=90°. 画出旋转后的图形:如图,将△ABC绕点O旋转后,顶点A的对应点为点D,试确定点B,C对应点的位置,并画出旋转后的三角形.
画出旋转后的图形:如图,将△ABC绕点O旋转后,顶点A的对应点为点D,试确定点B,C对应点的位置,并画出旋转后的三角形.