题目内容
5.已知二次函数y=x2+bx+c的图象经过点P(2,m),与x轴交于A(p,0),B(q,0),且0<p<q<2(1)若p=1,m=$\frac{1}{2}$,求函数的表达式并写出当y>0时的x的取值范围;
(2)求证:m>0;
(3)若c≥1,求m的取值范围.
分析 (1)点P、点A代入即可求出抛物线解析式;
(2)可以根据已知画出二次函数图象,根据图象分析可以证明m>0.
(3)利用二次函数交点式与一般式写出等式,根据特殊点带入,求出cm的一个代数式,通过展开代数式和代数式因式分解,即可证明m<1.
解答 解:(1)由二次函数y=x2+bx+c的图象经过点P(2,$\frac{1}{2}$)和点A(1,0),
可得$\left\{\begin{array}{l}{4+2b+c=\frac{1}{2}}\\{1+b+c=0}\end{array}\right.$,解得到$\left\{\begin{array}{l}{b=-\frac{5}{2}}\\{c=\frac{3}{2}}\end{array}\right.$,
∴抛物线解析式为y=x2-$\frac{5}{2}$x+$\frac{3}{2}$,
(2)∵二次函数y=x2+ax+b二次项系数为1,
∴二次函数图象抛物线开口向上.
∵二次函数y=x2+ax+b的图象经过点P(2,m),与x轴交于A(p,0),B(q,0),且0<p<q<2,如图: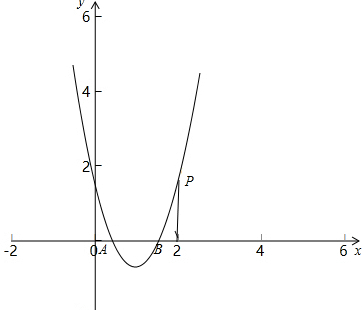
∴二次函数当x=q时,y=0,且x>q时,y随x的增大而增大,
∴m>0;
(3)由已知得:x2+ax+b=(x-p)(x-q),
令x=0得c=pq,
令x=2得m=(2-p)(2-q),
∴cm=pq(2-p)(2-q)=[1-(x-p)2][1-(q-1)2],
∵0<p<q<2,
0<1-(x-p)2<1,0<1-(q-1)2<1,
并且1-(x-p)2=1和1-(q-1)2=1不能同时成立,
∴0<cm<1,
又∵c≥1,
∴m<1.
点评 考查了待定系数法求二次函数的经销商以及二次函数图象与坐标轴交点知识,同时考查学生分析问题解决问题能力,特别是代数式的变形,更能看出本题作为奥数解答题的重要性.

 如图是一个轴对称图形,解答下列问题:
如图是一个轴对称图形,解答下列问题: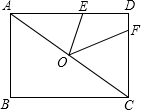 如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO.
如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO. 画出旋转后的图形:如图,将△ABC绕点O旋转后,顶点A的对应点为点D,试确定点B,C对应点的位置,并画出旋转后的三角形.
画出旋转后的图形:如图,将△ABC绕点O旋转后,顶点A的对应点为点D,试确定点B,C对应点的位置,并画出旋转后的三角形.