题目内容
2. 作图题:
作图题:①请在右图中画一条长为$\sqrt{13}$的线段AB;
②请在右图画一个三边长分别为$\sqrt{10}$,$\sqrt{5}$,5个单位的△DEF.
分析 ①因为22+32=($\sqrt{13}$)2,所以两条直角边分别为2、3,画出斜边就是$\sqrt{13}$;
②因为12+32=($\sqrt{10}$)2,22+12=($\sqrt{5}$)2,42+32=52,所以分别找出两个直角边,画出斜边,连接组成三边长分别为$\sqrt{10}$,$\sqrt{5}$,5个单位的△DEF.
解答 解:如图,
点评 此题考查勾股定理的实际运用,抓住能把斜边的平方分成两个自然数的平方和是解决问题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
17.请你按下列程序进行计算,把答案填写在表格内,然后看看有什么规律,想想为什么会有这样的规律?

(1)填写表内的空格:
(2)你发现的规律是:(n2+n)÷n-n=1.

(1)填写表内的空格:
| 输入 n | 3 | 2 | -2 | $\frac{1}{3}$ | … |
| 输出答案y | 1 | 1 | 1 | 1 | … |
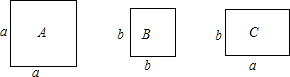 如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼成一个长为a+2b,宽为a+b的大长方形,则需要A、B、C类卡片各多少张?
如图,正方形卡片A类、B类和长方形卡片C类各有若干张,如果要拼成一个长为a+2b,宽为a+b的大长方形,则需要A、B、C类卡片各多少张? 如图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出这个几何体的主视图和左视图.
如图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请画出这个几何体的主视图和左视图.