题目内容

1．正多边形的每个内角都等于135°，则该多边形是正八边形．

分析 首先根据多边形的内角与相邻的外角互补可得外角为180°-135°=45°，再利用外角和360°除以外角的度数可得边数．

解答 解：∵正多边形的每个内角都等于135°，
∴多边形的外角为180°-135°=45°，
∴多边形的边数为360°÷45°=8，
故答案为：八．

点评 此题主要考查了多边形的内角与外角，关键是掌握外角和360°除以外角的度数可得边数．

练习册系列答案
相关题目
11．不等式 $\left\{\begin{array}{l}{x＜2}\\{x＞1}\end{array}\right.$的解集是（　　）
A．x＜2B．1＜x＜2C．x＞1D．x＞-2
12．如图，如果AE∥DF，求∠A+∠B+∠C+∠D=180°．
9．某政府大力扶持大学生创业，李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯，物价部门规定，这种护眼台灯的销售单价不得高于32元．销售过程中发现，月销售量y（件）与销售单价x（元）之间的关系可看作一次函数：y=-10x+n．
（1）当销售单价x定为25元时，李明每月获得利润w为1250元，求n的值；
（2）当销售单价定为多少元时，每月可获得最大利润？并求最大利润是多少？
16．化简：$\frac{{{m^2}-2m}}{{{m^3}+{m^2}-6m}}$==$\frac{1}{m+3}$．
6．根据给出的数轴，解答下面的问题：
（1）请你根据图中A、B（在-2，-3的正中间）两点的位置，分别写出它们所表示的有理数A：1     B：-2.5
（2）在数轴上画出与点A的距离为2的点（用不同于A、B、M、N的其他字母表示），并写出这些点表示的数：-1或3
（3）若经过折叠，A点与-3表示的点重合，则B点与数0.5表示的点重合；
（4）若数轴上M、N两点之间的距离为2016（M在N的左侧），且M、N两点经过（3）中折叠后重合，M、N两点表示的数分别是：M：-1009  N：1007．
13．在-2.4，3，-$\frac{10}{3}$，1$\frac{1}{4}$，-0.$\stackrel{•}{1}$$\stackrel{•}{5}$，0，-（-2.28），π，-|-4|，2.010010001…中，负数有4个，负分数有3个，无理数有2个．
10．点P到⊙O上各点的最大距离为5，最小距离为1，则⊙O的半径为3或2．
11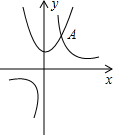．如图，抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2，则关于x的不等式$\frac{k}{x}$+x2+2＜0的解是（　　）
A．0＜x＜2B．-2＜x＜0C．x＞2D．x＜-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网