题目内容
12．
如图，如果AE∥DF，求∠A+∠B+∠C+∠D=180°．
分析 先由三角形外角的性质得出∠C+∠D=∠DMN，再根据平行线的性质得出∠DMN=∠ANB，根据三角形内角和定理即可得出结论．
解答 
解：∵∠DMN是△CDM的外角，
∴∠C+∠D=∠DMN．
∵AE∥DF，
∴∠DMN=∠ANB．
∵∠ANB+∠A+∠B=180°，
∴∠A+∠B+∠C+∠D=180°．
故答案为：180°．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
2．在-1和2之间的数是（ ）
| A． | -3 | B． | -2 | C． | 0 | D． | 3 |
3．
如图，△ABC≌△ADE，若∠B=70°，∠C=30°，∠DAC=35°，则∠EAC的度数为（ ）
如图，△ABC≌△ADE，若∠B=70°，∠C=30°，∠DAC=35°，则∠EAC的度数为（ ）| A． | 40° | B． | 45° | C． | 35° | D． | 25° |
20．下列分式约分正确的是（ ）
| A． | $\frac{{a}^{6}}{{a}^{3}}$=a2 | B． | $\frac{x+y}{x-y}$=1 | C． | $\frac{2a{b}^{2}}{6{a}^{2}b}$=$\frac{1}{3}$ | D． | $\frac{m+n}{{m}^{2}+mn}$=$\frac{1}{m}$ |
如图，△ABC≌△DEF，∠A=37°，∠E=38°，则∠ACE的度数为75°．
4．
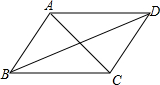如图，AB∥CD，AD∥BC，则图中全等三角形的组数是（ ）
如图，AB∥CD，AD∥BC，则图中全等三角形的组数是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
