题目内容
16.化简:$\frac{{{m^2}-2m}}{{{m^3}+{m^2}-6m}}$==$\frac{1}{m+3}$.分析 先提取公因式,再进行因式分解,然后约去分子、分母中相同的因式,即可得出答案.
解答 解:$\frac{{{m^2}-2m}}{{{m^3}+{m^2}-6m}}$=$\frac{m(m-2)}{m({m}^{2}+m-6)}$=$\frac{1}{m+3}$;
故答案为:$\frac{1}{m+3}$.
点评 此题考查了约分,约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.

练习册系列答案
相关题目
4.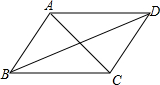 如图,AB∥CD,AD∥BC,则图中全等三角形的组数是( )
如图,AB∥CD,AD∥BC,则图中全等三角形的组数是( )
 如图,AB∥CD,AD∥BC,则图中全等三角形的组数是( )
如图,AB∥CD,AD∥BC,则图中全等三角形的组数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
11.下列计算结果正确的是( )
| A. | $\frac{1}{a+3}$-$\frac{1}{a-3}$=$\frac{1}{{a}^{2}-9}$ | |
| B. | $\frac{2x}{{x}^{2}-4}$-$\frac{1}{x+2}$=$\frac{1}{x-2}$ | |
| C. | $\frac{1}{{a}^{2}-{b}^{2}}$-$\frac{1}{{b}^{2}-{a}^{2}}$=$\frac{2{a}^{2}}{({a}^{2}-{b}^{2})({b}^{2}-{a}^{2})}$ | |
| D. | $\frac{x-6}{{x}^{2}-4}$+$\frac{1}{2-x}$=$\frac{2x-4}{{x}^{2}-4}$ |
8.下列做法错误的是( )
| A. | 小丽近6个月的手机话费(单位:元)分别为:18,24,37,28,24,26,这组数据的中位数是25 | |
| B. | 服装店老板最关心的是卖出服装的众数 | |
| C. | 要了解全市初中毕业班近4万名学生2015年中考数学成绩情况,适宜采用全面调查 | |
| D. | 条形统计图能够显示每组中的具体数据,易于比较数据之间的差别 |

 如图,△ABC≌△DEF,∠A=37°,∠E=38°,则∠ACE的度数为75°.
如图,△ABC≌△DEF,∠A=37°,∠E=38°,则∠ACE的度数为75°.