题目内容
15.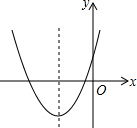 抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a-b+c>0;④b2-4ac<0;⑤abc<0;⑥4a>c;其中正确的为( )
抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a-b+c>0;④b2-4ac<0;⑤abc<0;⑥4a>c;其中正确的为( )| A. | ①②⑥ | B. | ①④ | C. | ①②③ | D. | ①③⑤ |
分析 由抛物线的开口向上知a>0,与y轴的交点为在y轴的正半轴上得到c>0,由此判定①正确;
由4a=b和对称轴为x=-$\frac{b}{2a}$=-2,∴a、b同号,即b>0,然后即可判定⑤错误;
由抛物线与x轴有两个交点得到b2-4ac>0,由此判定④错误;
当x=1时,y=a+b+C>0,由此判定②正确;
当x=-1时,y=a-b+c<0,由此判定③错误;
由图象知道a-b+c<0,而2a=b,可以推出c<a,进一步得到4a>c,由此判定⑥正确.
解答 解:∵抛物线的开口向上,
∴a>0,
∵与y轴的交点为在y轴的正半轴上,
∴c>0,
∴①正确;
∵对称轴为x=-$\frac{b}{2a}$且b=4a,x=-2,
∴a、b同号,即b>0,
∴abc>0,
∴⑤错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴④错误;
当x=1时,y=a+b+C>0,
∴②正确;
当x=-1时,y=a-b+c<0,
∴③错误;
∵a-b+c<0,4a=b,
∴c<3a,
∴4a>c,
∴⑥正确.
故选A.
点评 本题考查了二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定:
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0;
(2)b由对称轴和a的符号确定:由对称轴公式判断符号;
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0;
(4)b2-4ac由抛物线与x轴交点的个数确定:
①2个交点,b2-4ac>0;
②1个交点,b2-4ac=0;
③没有交点,b2-4ac<0.
(5)当x=1时,可以确定y=a+b+c的值;当x=-1时,可以确定y=a-b+c的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列函数:①y=2x-1,②y=$\frac{1}{x}$,③y=-3x,④y=x2+1.其中是一次函数的有( )
| A. | ① | B. | ①③ | C. | ①②③ | D. | ①③④ |
4.下列事件中,是不确定事件的是( )
| A. | 明年小刚的年龄比今年大一岁 | B. | 农历的春节在元旦之后 | ||
| C. | 任意买一张电影票座位号是偶数 | D. | 我市冬季的平均温度比夏季低 |
 如图,线段AB的长为l.
如图,线段AB的长为l. 某五金厂生产的螺母形状如图所示,
某五金厂生产的螺母形状如图所示,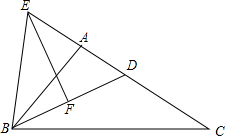 已知,在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于E,求证:∠EBA=∠C.
已知,在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于E,求证:∠EBA=∠C.